ĢāÄæÄŚČŻ
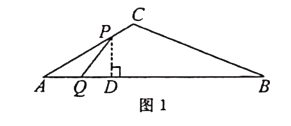
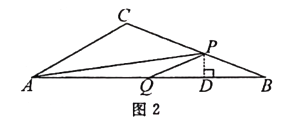
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚ”÷ABCÖŠ£¬”ĻA=30”ć£¬µćP“ÓµćA³ö·¢ŅŌ2cm/sµÄĖŁ¶ČŃŲÕŪĻßA”ŖC”ŖBŌĖ¶Æ£¬µćQ“ÓµćA³ö·¢ŅŌa(cm/s)µÄĖŁ¶ČŃŲABŌĖ¶Æ£¬P£¬QĮ½µćĶ¬Ź±³ö·¢£¬µ±Ä³Ņ»µćŌĖ¶Æµ½µćBŹ±£¬Į½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ.ÉčŌĖ¶ÆŹ±¼äĪŖx(s)£¬”÷APQµÄĆ껿ĪŖy(cm2)£¬y¹ŲÓŚxµÄŗÆŹżĶ¼ĻóÓÉC1 £¬ C2Į½¶Ī×é³É£¬ČēĶ¼2ĖłŹ¾.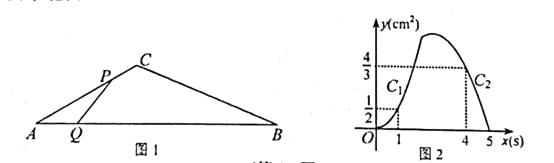
£Ø1£©ĒóaµÄÖµ£»
£Ø2£©ĒóĶ¼2ÖŠĶ¼ĻóC2¶ĪµÄŗÆŹż±ķ“ļŹ½£»
£Ø3£©µ±µćPŌĖ¶Æµ½Ļ߶ĪBCÉĻijŅ»¶ĪŹ±”÷APQµÄĆ껿£¬“óÓŚµ±µćPŌŚĻ߶ĪACÉĻČĪŅāŅ»µćŹ±”÷APQµÄĆ껿£¬ĒóxµÄȔֵ·¶Ī§.
”¾“š°ø”æ
£Ø1£©
½ā£ŗŌŚĶ¼1ÖŠ£¬¹żP×÷PD”ĶABÓŚD£¬”ß”ĻA=30”ć£¬PA=2x£¬
”ąPD=PA”¤sin30”ć=2x”¤ ![]() =x£¬
=x£¬
”ąy= ![]() =
= ![]() .
.
ÓÉĶ¼ĻóµĆ£¬µ±x=1Ź±£¬y= ![]() £¬Ōņ
£¬Ōņ ![]() =
= ![]() .
.
”ąa=1.
£Ø2£©
½ā£ŗµ±µćPŌŚBCÉĻŹ±£ØČēĶ¼2£©£¬PB=5”Į2-2x=10-2x.
”ąPD=PB”¤sinB=(10-2x)”¤sinB£¬
”ąy= ![]() AQ”¤PD=
AQ”¤PD= ![]() x”¤£Ø10-2x£©”¤sinB.
x”¤£Ø10-2x£©”¤sinB.
ÓÉĶ¼ĻóµĆ£¬µ±x=4Ź±£¬y= ![]() ,
,
”ą ![]() ”Į4”Į£Ø10-8£©”¤sinB=
”Į4”Į£Ø10-8£©”¤sinB= ![]() £¬
£¬
”ąsinB= ![]() .
.
”ąy= ![]() x”¤£Ø10-2x£©”¤
x”¤£Ø10-2x£©”¤ ![]() =
= ![]() .
.
£Ø3£©
½ā£ŗÓÉC1£¬C2µÄŗÆŹż±ķ“ļŹ½£¬µĆ ![]() =
= ![]() £¬
£¬
½āµĆx1=0£ØÉįČ„£©£¬x2=2£¬
ÓÉĶ¼Ņ×µĆ£¬µ±x=2Ź±£¬ŗÆŹży= ![]() µÄ×ī“óÖµĪŖy=
µÄ×ī“óÖµĪŖy= ![]() .
.
½«y=2“śČėŗÆŹży= ![]() £¬µĆ2=
£¬µĆ2= ![]() .
.
½āµĆx1=2£¬x2=3£¬
”ąÓÉĶ¼ĻóµĆ£¬xµÄȔֵ·¶Ī§ŹĒ2<x<3.
”¾½āĪö”æ£Ø1£©C1¶ĪµÄŗÆŹż½āĪöŹ½ŹĒµćPŌŚACĻ߶ĪŹ±yÓėxµÄ¹ŲĻµ£¬ÓÉS= ![]() AQ”¤£ØAQÉĻµÄøߣ©£¬¶ųAQ=ax£¬ÓÉ”ĻA=30”ć£¬PA=2x£¬æɹżP×÷PD”ĶABÓŚD£¬ŌņPD=PA”¤sin30”ć=2x”¤
AQ”¤£ØAQÉĻµÄøߣ©£¬¶ųAQ=ax£¬ÓÉ”ĻA=30”ć£¬PA=2x£¬æɹżP×÷PD”ĶABÓŚD£¬ŌņPD=PA”¤sin30”ć=2x”¤ ![]() =x£¬ŌņæÉŠ“³öy¹ŲÓŚxµÄ½āĪöŹ½£¬“śČėµć£Ø1£¬
=x£¬ŌņæÉŠ“³öy¹ŲÓŚxµÄ½āĪöŹ½£¬“śČėµć£Ø1£¬ ![]() £©£¬¼“æÉĒó³ösinB£¬¼“æɽā“š£»£Ø3£©ĢāÖŠ±ķŹ¾ŌŚÄ³xµÄȔֵ·¶Ī§ÄŚC1<C2 £¬ ¼““ĖŹ±C2µÄyÖµ“óÓŚC1µÄyÖµµÄ×ī“óÖµ£¬ÓÉĶ¼Ņ×µĆ£¬µ±x=2Ź±£¬ŗÆŹży=
£©£¬¼“æÉĒó³ösinB£¬¼“æɽā“š£»£Ø3£©ĢāÖŠ±ķŹ¾ŌŚÄ³xµÄȔֵ·¶Ī§ÄŚC1<C2 £¬ ¼““ĖŹ±C2µÄyÖµ“óÓŚC1µÄyÖµµÄ×ī“óÖµ£¬ÓÉĶ¼Ņ×µĆ£¬µ±x=2Ź±£¬ŗÆŹży= ![]() µÄ×ī“óÖµĪŖy=
µÄ×ī“óÖµĪŖy= ![]() .½«y=2“śČėŗÆŹży=
.½«y=2“śČėŗÆŹży= ![]() £¬Ēó³öxµÄÖµ£¬øł¾ŻŗÆŹży=
£¬Ēó³öxµÄÖµ£¬øł¾ŻŗÆŹży= ![]() £¬µÄæŖæŚĻņĻĀ£¬ŌņæɵĆxµÄȔֵ·¶Ī§.
£¬µÄæŖæŚĻņĻĀ£¬ŌņæɵĆxµÄȔֵ·¶Ī§.
”¾æ¼µć¾«Īö”æ¹ŲÓŚ±¾Ģāæ¼²éµÄ¶ž“ĪŗÆŹżµÄĶ¼ĻóŗĶ¶ž“ĪŗÆŹżµÄŠŌÖŹ£¬ŠčŅŖĮĖ½ā¶ž“ĪŗÆŹżĶ¼Ļń¹Ų¼üµć£ŗ1”¢æŖæŚ·½Ļņ2”¢¶Ō³ĘÖį 3”¢¶„µć 4”¢ÓėxÖį½»µć 5”¢ÓėyÖį½»µć£»Ōö¼õŠŌ£ŗµ±a>0Ź±£¬¶Ō³ĘÖį×ó±ß£¬yĖęxŌö“ó¶ų¼õŠ”£»¶Ō³ĘÖįÓŅ±ß£¬yĖęxŌö“ó¶ųŌö“ó£»µ±a<0Ź±£¬¶Ō³ĘÖį×ó±ß£¬yĖęxŌö“ó¶ųŌö“󣻶Ō³ĘÖįÓŅ±ß£¬yĖęxŌö“ó¶ų¼õŠ”²ÅÄÜµĆ³öÕżČ·“š°ø£®