题目内容
如图,四边形 内接于⊙
内接于⊙ ,
, 是⊙
是⊙ 的直径,
的直径, ,垂足为
,垂足为 ,
, 平分
平分 .
.

(1)求证: 是⊙
是⊙ 的切线;
的切线;
(2)若 ,求
,求 的长.
的长.
【答案】
(1)证明见解析;(2)BD的长是4cm.
【解析】
试题分析:(1)连接OA,根据角之间的互余关系可得∠OAE=∠DEA=90°,故AE⊥OA,即AE是⊙O的切线;
(2)根据圆周角定理,可得在Rt△AED中,∠AED=90°,∠EAD=30°,有AD=2DE;在Rt△ABD中,∠BAD=90°,∠ABD=30°,有BD=2AD=4DE,即可得出答案.
试题解析:(1)连接OA,

∵DA平分∠BDE,
∴∠BDA=∠EDA.
∵OA=OD,
∴∠ODA=∠OAD,
∴∠OAD=∠EDA,
∴OA∥CE.
∵AE⊥DE,
∴∠AED=90°.
∴∠OAE=∠DEA=90°.
∴AE⊥OA.
∴AE是⊙O的切线;
(2)∵BD是直径,
∴∠BCD=∠BAD=90°.
∵∠DBC=30°,∠BDC=60°,
∴∠BDE=120°.
∵DA平分∠BDE,
∴∠BDA=∠EDA=60°.
∴∠ABD=∠EAD=30°.
∵在Rt△AED中,∠AED=90°,∠EAD=30°,
∴AD=2DE.
∵在Rt△ABD中,∠BAD=90°,∠ABD=30°,
∴BD=2AD=4DE.
∵DE的长是1cm,
∴BD的长是4cm.
考点:1.切线的判定,2.圆周角定理.

练习册系列答案
相关题目
 内接于⊙O,
内接于⊙O, ,
, 是⊙O上与点
是⊙O上与点 关于圆心
关于圆心 成中心对称的点,
成中心对称的点, 是
是 边上一点,连结
边上一点,连结 .已知
.已知 ,
, ,
, 是线段
是线段 上一动点,连结
上一动点,连结 并延长交四边形
并延长交四边形 的一边于点
的一边于点 ,且满足
,且满足 ,则
,则 的值为_______________.
的值为_______________. 内接于⊙O,
内接于⊙O,  为⊙O的直径,
为⊙O的直径, , 点
, 点 是
是 上一个动点,连结
上一个动点,连结 、
、 和
和 ,
,  相交于点
相交于点 , 过点
, 过点 作
作 于
于 与
与 ,连结
,连结 和
和 .
.
 ;
; , 求证:
, 求证: ;
; , 四边形
, 四边形 的面积为
的面积为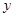 ,求
,求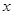 之间的关系式.
之间的关系式. 内接于⊙O,
内接于⊙O,  为⊙O的直径,
为⊙O的直径, , 点
, 点 是
是 上一个动点,连结
上一个动点,连结 、
、 和
和 ,
,  相交于点
相交于点 , 过点
, 过点 作
作 于
于 与
与 ,连结
,连结 和
和 .
.
 ;
; , 求证:
, 求证: ;
; , 四边形
, 四边形 的面积为
的面积为 ,求
,求 之间的关系式.
之间的关系式.