题目内容
在△ABC中，D为AB的中点，E为AC上一点，CE=
AC，BE、CD交于点O，BE=5cm，则OE= cm．
【答案】分析：过D作DF∥BE，由于D是AB中点，那么DF就是△ABE的中位线，利用三角形中位线定理，可求DF，而CE=
AC，AF=EF，可证出CE=EF，即E是CF中点，再次使用三角形中位线定理，可求出OE．
解答：
解：如图，过D作DF∥BE，那么DF就是三角形ABE的中位线，
∴DF=
BE，AF=EF
又∵CE=
AC
∴CE=EF
∴OE就是三角形CDF的中位线，
∴OE=
DF=
BE=1.25cm．
故答案为1.25．
点评：本题主要考查了三角形中位线的应用，根据题中给出的条件正确地作出中位线是解题的关键．
AC，AF=EF，可证出CE=EF，即E是CF中点，再次使用三角形中位线定理，可求出OE．解答：
解：如图，过D作DF∥BE，那么DF就是三角形ABE的中位线，∴DF=
BE，AF=EF又∵CE=
AC∴CE=EF
∴OE就是三角形CDF的中位线，
∴OE=
DF=BE=1.25cm．故答案为1.25．
点评：本题主要考查了三角形中位线的应用，根据题中给出的条件正确地作出中位线是解题的关键．
练习册系列答案
相关题目
已知：如图，在△ABC中，AD为BC边上的高，∠B=45°，∠C=30°，AD=2．求△ABC的面积．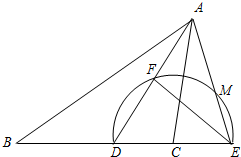
AD于点F，交AE于点M，且∠B=∠CAE，FE：FD=4：3．
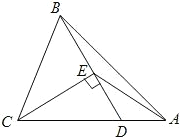
如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC面积是76cm2，AB=20cm，AC=18cm，求DE的长．