题目内容
如图,二次函数y=-| 1 |
| 2 |
| 3 |
| 9 |
| 2 |
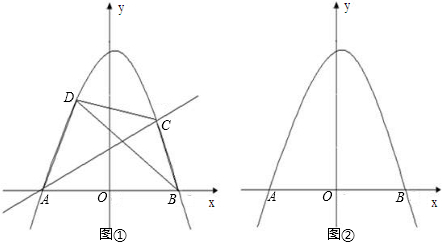
(1)求c的值;
(2)如图①,设点C为该二次函数的图象在x轴上方的一点,直线AC将四边形ABCD的面积二等分,试证明线段BD被直线AC平分,并求此时直线AC的函数解析式;
(3)设点P、Q为该二次函数的图象在x轴上方的两个动点,试猜想:是否存在这样的点P、Q,使△AQP≌△ABP?如果存在,请举例验证你的猜想;如果不存在,请说明理由.(图②供选用)
分析:(1)将D点坐标代入抛物线的解析式中,即可求出待定系数c的值;
(2)若△ACD与△ABC的面积相等,则两个三角形中,AC边上的高相等,设AC、BD的交点为E,若以CE为底,AC边上的高为高,可证得△CED和△CEB的面积相等;这两个三角形中,若以DE、BE为底,则两个三角形同高,那么DE=BE,由此可证得AC平分BD;
由于E是BD的中点,根据B、D的坐标,即可求出E点的坐标,根据A、E的坐标即可用待定系数法求出直线AC的解析式;
(3)设抛物线顶点为N(0,6),在Rt△AON中,易得AN=4
,于是以A点为圆心,AB=4
为半径作圆与抛物线在x轴上方一定有交点Q,连接AQ,再作∠QAB平分线AP交抛物线于P,连接BP,PQ,此时由“边角边”易得△AQP≌△ABP.
(2)若△ACD与△ABC的面积相等,则两个三角形中,AC边上的高相等,设AC、BD的交点为E,若以CE为底,AC边上的高为高,可证得△CED和△CEB的面积相等;这两个三角形中,若以DE、BE为底,则两个三角形同高,那么DE=BE,由此可证得AC平分BD;
由于E是BD的中点,根据B、D的坐标,即可求出E点的坐标,根据A、E的坐标即可用待定系数法求出直线AC的解析式;
(3)设抛物线顶点为N(0,6),在Rt△AON中,易得AN=4
| 3 |
| 3 |
解答: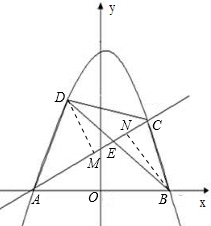 解:(1)∵抛物线经过D(-
解:(1)∵抛物线经过D(-
,
),则有
-
×3+c=
,
解得c=6;
(2)设AC与BD的交点为E,过D作DM⊥AC于M,过B作BN⊥AC于N
∵S△ADC=S△ACB,
∴
AC•DM=
AC•BN,即DM=BN;
∴
CE•DM=
CE•BN,
即S△CED=S△BEC(*);
设△BCD中,BD边上的高为h,由(*)得:
DE•h=
BE•h,即BE=DE,故AC平分BD;
易知:A(-2
,0),B(2
,0),D(-
,
),
由于E是BD的中点,则E(
,
);
设直线AC的解析式为y=kx+b,则有:
,
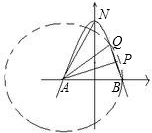 解得
解得
;
∴直线AC的解析式为y=
x+
(3)存在.
设抛物线顶点为N(0,6),在Rt△AON中,易得AN=4
,
于是以A点为圆心,AB=4
为半径作圆与抛物线在x轴上方一定有交点Q,连接AQ,
再作∠QAB平分线AP交抛物线于P,连接BP,PQ,
此时由“边角边”易得△AQP≌△ABP.
 解:(1)∵抛物线经过D(-
解:(1)∵抛物线经过D(-| 3 |
| 9 |
| 2 |
-
| 1 |
| 2 |
| 9 |
| 2 |
解得c=6;
(2)设AC与BD的交点为E,过D作DM⊥AC于M,过B作BN⊥AC于N
∵S△ADC=S△ACB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
即S△CED=S△BEC(*);
设△BCD中,BD边上的高为h,由(*)得:
| 1 |
| 2 |
| 1 |
| 2 |
易知:A(-2
| 3 |
| 3 |
| 3 |
| 9 |
| 2 |
由于E是BD的中点,则E(
| ||
| 2 |
| 9 |
| 4 |
设直线AC的解析式为y=kx+b,则有:
|
 解得
解得
|
∴直线AC的解析式为y=
3
| ||
| 10 |
| 9 |
| 5 |
(3)存在.
设抛物线顶点为N(0,6),在Rt△AON中,易得AN=4
| 3 |
于是以A点为圆心,AB=4
| 3 |
再作∠QAB平分线AP交抛物线于P,连接BP,PQ,
此时由“边角边”易得△AQP≌△ABP.
点评:此题主要考查了一次函数与二次函数解析式的确定、三角形面积的求法、以及全等三角形和直角三角形的判定和性质.

练习册系列答案
相关题目
 如图,二次函数的图象经过点D(0,
如图,二次函数的图象经过点D(0,
 如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题: 如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b
如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b