题目内容
（2004•泰安）不等式组
的整数解的个数是
|
8
8
．分析：分别求出不等式组中两不等式的解集，找出解集的公共部分，确定出不等式组的解集，找出解集中的整数解的个数即可．
解答：解：
，
由①去括号得：x-3x+6≤4，
解得：x≥2，
由②去分母得：1-2x＜20-4x，
解得：x＜
，
故不等式组的解集为2≤x＜
，
则不等式组的整数解为：2，3，4，5，6，7，8，9共8个．
故答案为：8．
|
由①去括号得：x-3x+6≤4，
解得：x≥2，
由②去分母得：1-2x＜20-4x，
解得：x＜
| 19 |
| 2 |
故不等式组的解集为2≤x＜
| 19 |
| 2 |
则不等式组的整数解为：2，3，4，5，6，7，8，9共8个．
故答案为：8．
点评：此题考查了一元一次不等式组的整数解，求出不等式组的解集是解本题的关键．
练习册系列答案
特高级教师点拨系列答案
相关题目
（2004•泰安）如图，在△ABC中，AB=3，BC=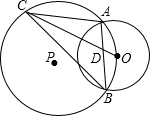
（2004•泰安）已知：如图，⊙P与⊙O相交于点A、B，且⊙P经过点O，点C是⊙P的优弧AB上任意一点（不与点A、B重合），弦OC交公共弦AB于点D，连接CA、CB．