Question

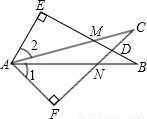
（2003•广州）如图，∠E=∠F=90°，∠B=∠C，AE=AF，给出下列结论：（1）∠1=∠2；（2）BE=CF；（3）△ACN≌△ABM；（4）CD=DN，其中正确的结论是    ．
（注：将你认为正确的结论都填上）．

Answer 1

【答案】分析：根据题目条件，利用AAS可以判断△AEB≌△AFC，由全等的性质对结论进行判断．
解答：解：∵∠E=∠F=90°，∠B=∠C，AE=AF
∴△AEB≌△AFC（AAS），
∴BE=CF
故（2）正确；
∵∠1=∠EAB-∠CAB，∠2=∠FAC-∠CAB
又∵∠EAB=∠FAC
∴∠1=∠2
故（1）正确；
∵AC=AB，∠B=∠C，∠CAN=∠BAM
∴△ACN≌△ABM（SAS）故（3）正确．
∴正确的结论是∠1=∠2，BE=CF，△ACN≌△ABM．
故填∠1=∠2，BE=CF，△ACN≌△ABM．
点评：本题考查了全等三角形的判定与性质；题目是全等三角形的判定、性质的综合运用，要求学生能熟练运用性质解题．