题目内容
（2003•广州）如图，已知△ABC内接于⊙O，直线DE与⊙O相切于点A，BD∥CA，求证：AB•DA=BC•BD．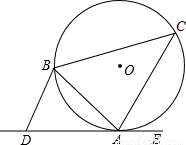
【答案】分析：欲证AB•DA=BC•BD，即证AB：BD=BC：DA，即证△ABC∽△BDA．根据已知条件，△ABC与△BDA中，有两角对应相等，由相似三角形的判定，它们相似．
解答：
证明：∵DE与⊙O相切，
∴∠C=∠1，
∵BD∥CA，∴∠2=∠3．
∴△ABC∽△BDA．
∴
．
∴AB•DA=BC•BD．
点评：本题考查相似三角形的判定定理：有两角对应相等的两个三角形相似．
解答：
证明：∵DE与⊙O相切，∴∠C=∠1，
∵BD∥CA，∴∠2=∠3．
∴△ABC∽△BDA．
∴
．∴AB•DA=BC•BD．
点评：本题考查相似三角形的判定定理：有两角对应相等的两个三角形相似．
练习册系列答案
相关题目
