题目内容
小明在解答题目“已知x=2+ ,求x3-4x2+3x+1的值”时,觉得如果将x的值直接代入,计算太繁,不易求解.与同学讨论后发现了如下解法:将已知条件x=2+
,求x3-4x2+3x+1的值”时,觉得如果将x的值直接代入,计算太繁,不易求解.与同学讨论后发现了如下解法:将已知条件x=2+ ;变形为x-2=
;变形为x-2= ,再将两边平方,得x2-4x+1=0,所以x3-4x2+3x+1=x3-4x2+x+2x+1=x(x2-4x+1)+2(x-2)+5=2
,再将两边平方,得x2-4x+1=0,所以x3-4x2+3x+1=x3-4x2+x+2x+1=x(x2-4x+1)+2(x-2)+5=2 +5.
+5.
请你仿照上面的做法,解决以下问题:
已知x=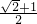 ,求代数式4x4+4x3-9x2-2x+1的值.
,求代数式4x4+4x3-9x2-2x+1的值.
解:∵x=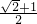 ,
,
∴2x= +1,即2x-1=
+1,即2x-1= ,
,
两边平方,得:4x2-4x=1,
则4x4+4x3-9x2-2x+1
=4x4-4x3+8x3-9x2-2x+1
=x2(4x2-4x)+8x3-9x2-2x+1
=x2+8x3-9x2-2x+1
=8x3-8x2-2x+1
=2x(4x2-4x)-2x+1
=2x-2x+1
=1.
分析:x=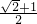 则2x=
则2x= +1,即2x-1=
+1,即2x-1= ,两边平方,得:4x2-4x=1,然后把所求的式子利用4x2-4x表示出来,代入求解即可.
,两边平方,得:4x2-4x=1,然后把所求的式子利用4x2-4x表示出来,代入求解即可.
点评:本题考查的是整式的混合运算,以及二次根式的化简求值,正确对所求的式子进行变形是关键.
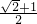 ,
,∴2x=
 +1,即2x-1=
+1,即2x-1= ,
,两边平方,得:4x2-4x=1,
则4x4+4x3-9x2-2x+1
=4x4-4x3+8x3-9x2-2x+1
=x2(4x2-4x)+8x3-9x2-2x+1
=x2+8x3-9x2-2x+1
=8x3-8x2-2x+1
=2x(4x2-4x)-2x+1
=2x-2x+1
=1.
分析:x=
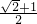 则2x=
则2x= +1,即2x-1=
+1,即2x-1= ,两边平方,得:4x2-4x=1,然后把所求的式子利用4x2-4x表示出来,代入求解即可.
,两边平方,得:4x2-4x=1,然后把所求的式子利用4x2-4x表示出来,代入求解即可.点评:本题考查的是整式的混合运算,以及二次根式的化简求值,正确对所求的式子进行变形是关键.

练习册系列答案
相关题目

 BC=BD=CD,
BC=BD=CD,