题目内容
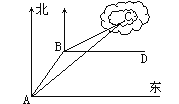
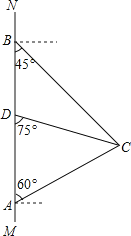
【题目】如图,在南北方向的海岸线![]() 上,有
上,有![]() 两艘巡逻船,现均收到故障船
两艘巡逻船,现均收到故障船![]() 的求救信号.已知
的求救信号.已知![]() 两船相距
两船相距![]() 海里,船
海里,船![]() 在船
在船![]() 的北偏东60°方向上,船
的北偏东60°方向上,船![]() 在船
在船![]() 的东南方向上,
的东南方向上, ![]() 上有一观测点
上有一观测点![]() ,测得船
,测得船![]() 正好在观测点
正好在观测点![]() 的南偏东75°方向上.
的南偏东75°方向上.
(1)分别求出![]() 与
与![]() ,
,![]() 与
与![]() 间的距离
间的距离![]() 和
和![]() ; (本问如果有根号,结果请保留根号) (此提示可以帮助你解题:∵
; (本问如果有根号,结果请保留根号) (此提示可以帮助你解题:∵![]() ,∴
,∴![]() )
)
(2)已知距观测点![]() 处100海里范围内有暗礁,若巡逻船
处100海里范围内有暗礁,若巡逻船![]() 沿直线
沿直线![]() 去营救船
去营救船![]() ,去营救的途中有无触礁的危险?(参考数据:
,去营救的途中有无触礁的危险?(参考数据: ![]() )
)
【答案】(1)![]() 与
与![]() 之间的距离
之间的距离![]() 为200海里,
为200海里, ![]() 与
与![]() 之间的距离
之间的距离![]() 为
为![]() 海里;(2)巡逻船
海里;(2)巡逻船![]() 沿直线
沿直线![]() 航线,在去营救的途中没有触暗礁危险.
航线,在去营救的途中没有触暗礁危险.
【解析】
(1)作CE⊥AB于E,设AE=x海里,则![]() 海里.根据
海里.根据![]() ,求得x的值后即可求得AC的长,过点D作DF⊥AC于点F,同理求出AD的长;
,求得x的值后即可求得AC的长,过点D作DF⊥AC于点F,同理求出AD的长;
(2)根据(1)中的结论得出DF的长,再与100比较即可得到答案.
解:(1)如图,
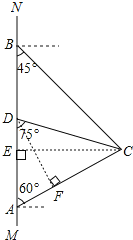
过点![]() 作
作![]() 于
于![]() ,设
,设![]() 海里,
海里,
过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() 海里,
海里,
由题意得: ![]() ,
,![]() ,
,
在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() .
.
∴![]() ,
,
解得: ![]() ,
,
∴![]() .
.
在![]() 中,
中, ![]() ,则
,则![]() .
.
则![]() .
.
∴![]() ,
,
解得: ![]() ,
,
∴AD=2y=![]()
答: ![]() 与
与![]() 之间的距离
之间的距离![]() 为200海里,
为200海里,![]() 与
与![]() 之间的距离
之间的距离![]() 为
为![]() 海里.
海里.
(2)由(1)可知, ![]() ,
,
≈126.3(海里),
∵![]() ,
,
∴巡逻船![]() 沿直线
沿直线![]() 航线,在去营救的途中没有触暗礁危险.
航线,在去营救的途中没有触暗礁危险.

练习册系列答案
相关题目
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
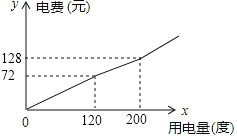
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?