题目内容
(本题满分11分.为方便答题,可在答卷上画出你认为必要的图形)
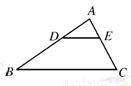
如图,已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是AD、BC、BE、CE的中点.

(1)求证:△ABE≌△DCE;
(2)四边形EGFH是什么特殊四边形?并证明你的结论.
(3)连接EF,当四边形EGFH是正方形时,线段EF与BC有什么数量关系?请说明理由.
(1)证明详见解析;(2)四边形EGFH是菱形.证明详见解析;(3)EF⊥BC,且EF= BC,证明详见解析.
BC,证明详见解析.
【解析】
试题分析:(1)通过证明AE=ED,∠A=∠D, AB=DC,根据全等三角形的判定可以证得△ABE≌△DCE;
由题意可知GF、FH是△EBC的中位线,且EB=EC,所以GF∥EH,GE∥HF,GF=GE,从而证得四边形EGFH是菱形;
连接EF,证得△BEC是等腰直角三角形,从而得到EF⊥BC,且EF= BC.
BC.
试题解析:(1)证明:由题意可得ABCD是等腰梯形,
∴∠A=∠D,
在△ABE和△DCE中,AE=ED,∠A=∠D, AB=DC,
∴△ABE≌△DCE.
(2)四边形EGFH是菱形.
证明:∵GF、FH是△EBC的中位线,且由(1)得EB=EC,
∴GF∥EH,GE∥HF,GF=GE,
∴四边形EGFH是菱形.
(3)EF⊥BC,且EF= BC.
BC.
证明:连接EF,∵EFGH是正方形,
∴∠GEH=90°,即△BEC是等腰直角三角形,
∴EF⊥BC,且EF= BC.
BC.
考点:全等三角形的判定;三角形的中位线;菱形的判定;正方形的性质.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 向左平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )
向左平移2个单位,再向上平移2个单位,得到的抛物线解析式为( ) B.
B.
 D.
D.


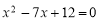 的两根,则这两个圆的位置关系是 .
的两根,则这两个圆的位置关系是 .