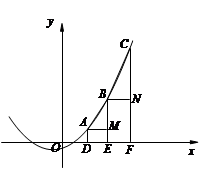题目内容
如图,抛物线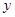 =-
=-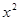 +5
+5 +
+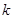 经过点C(4,0),与
经过点C(4,0),与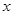 轴交于另一点A,与
轴交于另一点A,与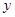 轴交于点B.
轴交于点B.
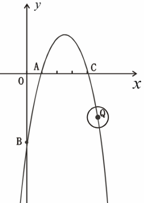
(1)求点A、B的坐标;
(2)P是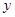 轴上一点,△PAB是等腰三角形,试求P点坐标;
轴上一点,△PAB是等腰三角形,试求P点坐标;
(3)若·Q的半径为1,圆心Q在抛物线上运动,当·Q与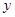 轴相切时,求·Q上的点到点B的最短距离.
轴相切时,求·Q上的点到点B的最短距离.
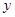 =-
=-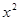 +5
+5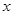 +
+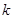 经过点C(4,0),与
经过点C(4,0),与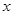 轴交于另一点A,与
轴交于另一点A,与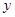 轴交于点B.
轴交于点B.
(1)求点A、B的坐标;
(2)P是
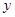 轴上一点,△PAB是等腰三角形,试求P点坐标;
轴上一点,△PAB是等腰三角形,试求P点坐标;(3)若·Q的半径为1,圆心Q在抛物线上运动,当·Q与
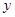 轴相切时,求·Q上的点到点B的最短距离.
轴相切时,求·Q上的点到点B的最短距离.(1)A(1,0),B(0,-4);(2)P1(0,4),P2(0,- ),P3(0,-4-
),P3(0,-4- );
);
(3) -1
-1
 ),P3(0,-4-
),P3(0,-4- );
);(3)
 -1
-1试题分析:(1)将C代入
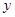 =-
=-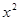 +5
+5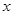 +
+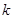 即可求得抛物线的解折式,再把
即可求得抛物线的解折式,再把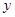 =0与
=0与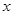 =0代入求得的抛物线的解折式即可求得结果;
=0代入求得的抛物线的解折式即可求得结果;(2)先根据题意作出图形,再根据等腰三角形的性质结合勾股定理求解即可;
(3)由题意当Q的横坐标为1或-1时成立,再代入抛物线解析式即可求得点Q的坐标,连Q1B(即AB),交⊙Q1于M. 连Q2B,交⊙Q2于N,MB和NB即为所求.
(1)将C代入抛物线的解折式得:0=-42+5×4+
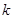 ,
,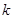 =-4,所以
=-4,所以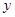 =-
=-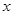 2+5
2+5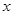 -4
-4令
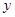 =0,则-
=0,则-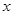 2+5
2+5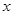 -4=0,解得
-4=0,解得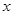 1=4,
1=4, 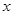 2=1,所以A(1,0)
2=1,所以A(1,0) 令
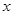 =0,则
=0,则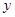 =-02+5×0-4=-4,所以B(0,-4);
=-02+5×0-4=-4,所以B(0,-4);(2)如图,P点有三个.

P1(0,4)
令∣P2B∣=
 . 则∣0P2∣=4-
. 则∣0P2∣=4-
∣P2A∣2=∣0P2∣2+∣0A∣2=(4-
 )2+12=
)2+12= 2,解得
2,解得 =
=
P2(0,-
 )
)∣BP3∣=AB=
 +
+ =
=
P3(0,-4-
 );
);(3)当Q的横坐标为1或-1时成立
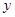 =-12+5×1-4=0. Q1(1,0)
=-12+5×1-4=0. Q1(1,0)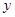 =-(-1)2+5×(-1)-4=-10,Q2(-1,-10)
=-(-1)2+5×(-1)-4=-10,Q2(-1,-10)连Q1B(即AB),交⊙Q1于M. 连Q2B,交⊙Q2于N,MB和NB即为所求
MB=Q1B-Q1M=AB-QM=
 -1
-1 NB=Q2B-Q2N=
 -1=
-1= -1.
-1.点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目
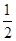 时,y随x的增大而减小;
时,y随x的增大而减小;
 米
米 的自变量x的取值范围是 .
的自变量x的取值范围是 . 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:① ;②
;② ;③当
;③当 时,
时, 的最小值为
的最小值为 ,④
,④ 中,正确的有 .
中,正确的有 .
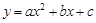 ,使它同时具有如下性质:
,使它同时具有如下性质: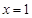 对称;②当x=2时,y>0;③当x=-2时,y<0.
对称;②当x=2时,y>0;③当x=-2时,y<0.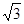 ,0),点D(0,1),CD的中垂线交CD于点E,交y轴于点B,点P从点C出发沿CO方向以每秒
,0),点D(0,1),CD的中垂线交CD于点E,交y轴于点B,点P从点C出发沿CO方向以每秒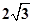 个单位的速度运动,同时点Q从原点O出发沿OD方向以每秒1个单位的速度向点D运动,当点Q到达点D时,点P,Q同时停止运动,设运动的时间为秒。
个单位的速度运动,同时点Q从原点O出发沿OD方向以每秒1个单位的速度向点D运动,当点Q到达点D时,点P,Q同时停止运动,设运动的时间为秒。
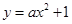 经过P′Q′的中点,此时的抛物线与x轴正半轴交于点M。由已知,直接写出:
经过P′Q′的中点,此时的抛物线与x轴正半轴交于点M。由已知,直接写出: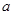 的取值范围为 ;
的取值范围为 ; ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为( ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.