Question

【题目】如图，点在线段上，在的同侧作角的直角三角形和角的直角三角形，与，分别交于点，，连接.对于下列结论：

①；②；③图中有5对相似三角形；④．其中结论正确的个数是(　　)

A.1个B.2个C.4个D.3个

Answer 1

【答案】D

【解析】

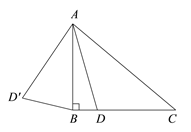
如图，设AC与PB的交点为N，根据直角三角形的性质得到，根据相似三角形的判定定理得到△BAE∽△CAD，故①正确；根据相似三角形的性质得到∠BEA＝∠CDA，推出△PME∽△AMD，根据相似三角形的性质得到MPMD＝MAME，故②正确；由相似三角形的性质得到∠APM＝∠DEM＝90，根据垂直的定义得到AP⊥CD，故④正确；同理：△APN∽△BCN，△PNC∽△ANB，于是得到图中相似三角形有6对，故③不正确．

如图，设AC与PB的交点为N，

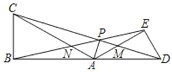
∵∠ABC＝∠AED＝90，∠BAC＝∠DAE＝30，

∴，∠BAE＝30＋∠CAE，∠CAD＝30＋∠CAE，

∴∠BAE＝∠CAD，

∴△BAE∽△CAD，故①正确；

∵△BAE∽△CAD，

∴∠BEA＝∠CDA，

∵∠PME＝∠AMD，

∴△PME∽△AMD，

∴，

∴MPMD＝MAME，故②正确；

∴，

∵∠PMA＝∠EMD，

∴△APM∽△DEM，

∴∠APM＝∠DEM＝90，

∴AP⊥CD，故④正确；

同理：△APN∽△BCN，△PNC∽△ANB，

∵△ABC∽△AED，

∴图中相似三角形有6对，故③不正确；

故选：D．