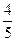题目内容
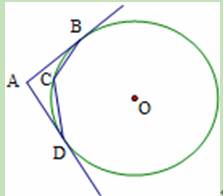
(2011•温州)如图,AB是⊙O的直径,弦CD⊥AB于点E,过点B作⊙O的切线,交AC的延长线于点F.已知OA=3,AE=2,
(1)求CD的长;
(2)求BF的长.
(1)求CD的长;
(2)求BF的长.

解:(1)如图:

连接OC,∵AB是直径,弦CD⊥AB,
∴CE=DE
在直角△OCE中,OC2=OE2+CE2
32=(3﹣2)2+CE2
得:CE=2 ,
,
∴CD=4 .
.
(2)∵BF切⊙O于点B,
∴∠ABF=90°=∠AEC
∴△ACE∽△AFB
∴ =
=
即: =
=
∴BF=6 .
.

连接OC,∵AB是直径,弦CD⊥AB,
∴CE=DE
在直角△OCE中,OC2=OE2+CE2
32=(3﹣2)2+CE2
得:CE=2
 ,
,∴CD=4
 .
.(2)∵BF切⊙O于点B,
∴∠ABF=90°=∠AEC
∴△ACE∽△AFB
∴
 =
=
即:
 =
=
∴BF=6
 .
.略

练习册系列答案
相关题目

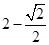 D.
D.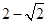
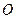 和⊙
和⊙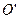 相交于
相交于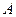 、
、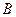 两点,过点
两点,过点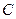 ,过点
,过点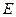 、
、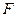 ,
,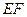 与
与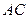 相交于点
相交于点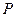 ,
, 1)求证:
1)求证: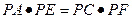 ;
;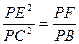 ;
;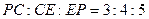 时,求
时,求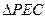 与
与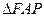 的面积的比值。
的面积的比值。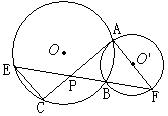
 是⊙
是⊙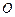 的直径,AC与⊙
的直径,AC与⊙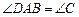 .
.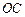 ∥
∥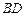 ;
;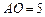 ,
,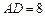 ,求线段CE的长.
,求线段CE的长.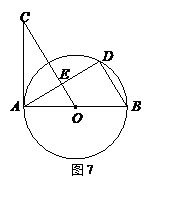
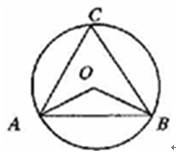
 上一点(不与O、A两点重合),则cosC的值为( )
上一点(不与O、A两点重合),则cosC的值为( )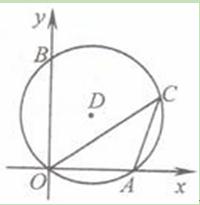
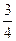 B.
B. C.
C.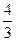 D.
D.