题目内容
己知a=2b-1，下列式子：①a+2=2b+1；②
=b；③3a=6b-1；④a-2b-1=0，其中一定成立的有（ ）
| a+1 |
| 2 |
| A、①② | B、①②③ |
| C、①②④ | D、①②③④ |
分析：根据等式的基本性质对四个小题进行逐一分析即可．
解答：解：①∵a=2b-1，∴a+2=2b-1+2，即a+2=2b+1，故此小题正确；
②∵a=2b-1，∴a+1=2b，∴
=b，故此小题正确；
③∵a=2b-1，∴3a=6b-3，故此小题错误；
④∵a=2b-1，∴a-2b+1=0，故此小题错误．
所以①②成立．
故选A．
②∵a=2b-1，∴a+1=2b，∴
| a+1 |
| 2 |
③∵a=2b-1，∴3a=6b-3，故此小题错误；
④∵a=2b-1，∴a-2b+1=0，故此小题错误．
所以①②成立．
故选A．
点评：本题考查的是等式的基本性质，熟知等式的基本性质是解答此题的关键．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
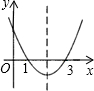己知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：（1）4a+2b+c＜0；（2）方程ax2+bx+c=0两根都大于零；（3）y随x的增大而增大；（4）一次函数y=x+bc的图象一定不过第二象限．其中正确的个数是（ ）
（任选一题，若两题都选按得分最少的题记分，本题最高10分）
=b；③3a=6b-1；④a-2b-1=0，其中一定成立的有
，
，求下列式的值
．