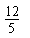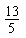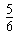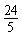题目内容
在同一平面上把三边BC=3,AC=4,AB=5的三角形沿最长边翻折成△ABC′,则CC′等于
- A.

- B.

- C.

- D.

D
分析:先根据勾股定理的逆定理判断出△ABC的形状,再画出图形,根据对称的性质可求出△ACD≌△ABC,再由全等三角形的对应边相等即可解答.
解答: 解:∵32+42=52,即:BC2+AC2=AB2,
解:∵32+42=52,即:BC2+AC2=AB2,
∴△ABC是直角三角形,斜边是AB,
由对称的性质可知:AB垂直且平分CC′,
设AB交CC′于D,则D是垂足,
∴CD=C′D,CC′=2CD;
∵∠CAD=∠CAB,∠ADC=∠ACB=90°,
∵△ACD∽△ABC,
∴ =
= ,
,
∴CD= =
= =
= ,
,
∴CC′=2CD= =
= .
.
故选D.
点评:本题考查的是图形翻折变换的性质,根据题意画出图形是解答此题的关键.
分析:先根据勾股定理的逆定理判断出△ABC的形状,再画出图形,根据对称的性质可求出△ACD≌△ABC,再由全等三角形的对应边相等即可解答.
解答:
 解:∵32+42=52,即:BC2+AC2=AB2,
解:∵32+42=52,即:BC2+AC2=AB2,∴△ABC是直角三角形,斜边是AB,
由对称的性质可知:AB垂直且平分CC′,
设AB交CC′于D,则D是垂足,
∴CD=C′D,CC′=2CD;
∵∠CAD=∠CAB,∠ADC=∠ACB=90°,
∵△ACD∽△ABC,
∴
 =
= ,
,∴CD=
 =
= =
= ,
,∴CC′=2CD=
 =
= .
.故选D.
点评:本题考查的是图形翻折变换的性质,根据题意画出图形是解答此题的关键.

练习册系列答案
相关题目
在同一平面上把三边BC=3,AC=4,AB=5的三角形沿最长边AB翻折后得到△ABC′,则CC′的长等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在同一平面上把三边BC=3,AC=4,AB=5的三角形沿最长边翻折成△ABC′,则CC′等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|