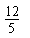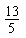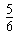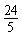题目内容
在同一平面上把三边BC=3，AC=4，AB=5的三角形沿最长边AB翻折后得到△ABC′，则CC′的长等于（ ）
A．
| B．
| C．
| D．
|
如图所示，
连接CC′，根据对称的性质可知CC′⊥AB，且CC'=2CE，
∵
AC×BC=
AB×CE，
∴CE=
，
∴CC′=2×CE=
．
故选D．
连接CC′，根据对称的性质可知CC′⊥AB，且CC'=2CE，
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CE=
| 12 |
| 5 |
∴CC′=2×CE=
| 24 |
| 5 |
故选D．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
在同一平面上把三边BC=3，AC=4，AB=5的三角形沿最长边AB翻折后得到△ABC′，则CC′的长等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在同一平面上把三边BC=3，AC=4，AB=5的三角形沿最长边翻折成△ABC′，则CC′等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
