题目内容
16.已知a,b,c分别为△ABC的三边的长,且满足a2+ab-ac-bc=b2+bc-ba-ca=0,则这个三角形的形状为( )| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等边三角形 | D. | 等边三角形或直角三角形 |
分析 根据a2+ab-ac-bc=b2+bc-ba-ca=0得到a2+ab-ac-bc=0,b2+bc-ba-ca=0,然后连续提取公因式即可得到(a+b)(a-c)=0,(b+c)(b-a)=0,再根据a+b≠0,b+c≠0得到a-c=0,b-a=0,从而得到a=c,b=a,得到该三角形为等边三角形.
解答 解:∵a2+ab-ac-bc=b2+bc-ba-ca=0,
∴a2+ab-ac-bc=0,b2+bc-ba-ca=0,
∴a(a+b)-c(a+b)=0,b(b+c)-a(b+c)=0
(a+b)(a-c)=0,(b+c)(b-a)=0
∵a+b≠0,b+c≠0,
∴a-c=0,b-a=0
∴a=c,b=a,
∴该三角形是等边三角形.
故选C.
点评 本题考查了因式分解的应用,解题的关键是能够对题目提供的式子进行因式分解,难度不大.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
4.若|a-1|+|b-2|=0,那么2ab=( )
| A. | -4 | B. | +4 | C. | -8 | D. | +8 |
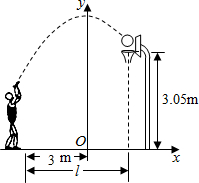 如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )
如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )