题目内容
 矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则折痕EF长度是
矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则折痕EF长度是
- A.

- B.

- C.

- D.

B
分析:首先连接AC,利用勾股定理计算出AC的长,进而得到CO的长,然后证明△DAC∽△OEC,根据相似三角形的性质可得 =
=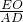 ,然后代入具体数值可得EO的长,进而得到答案.
,然后代入具体数值可得EO的长,进而得到答案.
解答: 解:连接AC,
解:连接AC,
∵折叠,使点A与点C重合,
∴AC⊥EF,AO=CO,
∵矩形ABCD,
∴∠D=90°,AC= =2
=2 ,
,
∴CO= ,
,
∵∠EOC=∠D=90°,∠ECO=∠DCA,
∴△DAC∽△OEC,
∴ =
=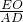 ,
,
∴ =
= ,
,
∴EO= ,
,
∴EF=2× =
= ,
,
故选:B.
点评:此题主要考查了图形的翻折变换,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
分析:首先连接AC,利用勾股定理计算出AC的长,进而得到CO的长,然后证明△DAC∽△OEC,根据相似三角形的性质可得
 =
=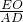 ,然后代入具体数值可得EO的长,进而得到答案.
,然后代入具体数值可得EO的长,进而得到答案.解答:
 解:连接AC,
解:连接AC,∵折叠,使点A与点C重合,
∴AC⊥EF,AO=CO,
∵矩形ABCD,
∴∠D=90°,AC=
 =2
=2 ,
,∴CO=
 ,
,∵∠EOC=∠D=90°,∠ECO=∠DCA,
∴△DAC∽△OEC,
∴
 =
=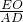 ,
,∴
 =
= ,
,∴EO=
 ,
,∴EF=2×
 =
= ,
,故选:B.
点评:此题主要考查了图形的翻折变换,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 如图,M为矩形纸片ABCD的边AD的中点,将纸片沿BM、CM折叠,使点A落在A1处,点D落在D1处.若∠A1MD1=40°,则∠BMC的度数为
如图,M为矩形纸片ABCD的边AD的中点,将纸片沿BM、CM折叠,使点A落在A1处,点D落在D1处.若∠A1MD1=40°,则∠BMC的度数为 其一面着色.
其一面着色.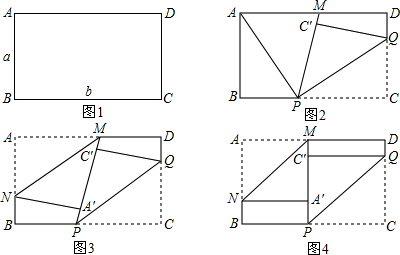
 如图,矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色.
如图,矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色. 已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD于点M,折痕交边BC于点N.
已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD于点M,折痕交边BC于点N.