题目内容
5.在正方形ABCD中,BD是一条对角线,点P在射线CD上(与点C、D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH.
(1)若点P在线段CD上,如图1.判断AH与PH的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,如图2.
①依题意补全图2;
②判断(1)中的结论是否还成立?若成立请直接写出结论;若不成立请说明理由.
分析 (1)连接HC,根据正方形的性质、等腰直角三角形的性质得到△HDP≌△HQC,根据全等三角形的性质得到HP=HC,∠DHP=∠QHC,根据正方形是轴对称图形证明结论;
(2)①根据题意画出图形即可;
②同(1)的证明方法相同,根据图形证明即可.
解答 解:(1)AH=PH,AH⊥PH,
理由如下:如图1,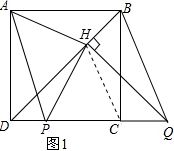 连接HC,
连接HC,
∵四边形ABCD是正方形,
∴∠BDC=45°,又QH⊥BD,
∴△DHQ是等腰直角三角形,
由平移的性质可知DP=CQ,
在△HDP和△HQC中,
$\left\{\begin{array}{l}{HD=HQ}\\{∠HDP=∠HQC}\\{DP=QC}\end{array}\right.$,
∴△HDP≌△HQC,
∴HP=HC,∠DHP=∠QHC,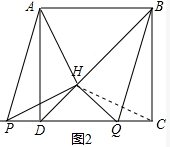
根据正方形是轴对称图形得到HA=HC,∠AHD=∠CHD,
∴HA=HP,AH⊥PH;
(2)①补全图见图2;
②如图2,连接HC,
根据正方形是轴对称图形得到HA=HC,∠AHD=∠CHD,
AH=PH,AH⊥PH,
理由如下:如图1,连接HC,
∵四边形ABCD是正方形,
∴∠BDC=45°,又QH⊥BD,
∴△DHQ是等腰直角三角形,
∴∠HDP=∠HQC=45°,
由平移的性质可知DP=CQ,
在△HDP和△HQC中,
$\left\{\begin{array}{l}{HD=HQ}\\{∠HDP=∠HQC}\\{PD=CQ}\end{array}\right.$,
∴△HDP≌△HQC,
∴HP=HC,∠DHP=∠QHC,
∴HA=HP,AH⊥PH.
点评 本题考查的是四边形综合题,涉及到正方形的性质、图形平移的性质、全等三角形的判定与性质等知识,难度适中,解决本题的关键是熟记全等三角形的性质定理和判定定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若函数y=(2m-1)${x}^{2-{m}^{2}}$+m+3是一次函数,且y随x的增大而减小,则m的值为( )
| A. | ±1 | B. | 1 | C. | -1 | D. | -3 |
13.下列代数式中,单项式共有( )
$\frac{3}{x}$,a-b,-2ab,$\frac{{x}^{2}+{y}^{2}}{5}$,0,$\frac{1}{2}$b2c3.
$\frac{3}{x}$,a-b,-2ab,$\frac{{x}^{2}+{y}^{2}}{5}$,0,$\frac{1}{2}$b2c3.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.若关于x,y的多项式$\frac{2}{5}{x^2}y-7mxy+\frac{3}{4}{y^3}+6xy$化简后不含二次项,则m=( )
| A. | $\frac{1}{7}$ | B. | $\frac{6}{7}$ | C. | $-\frac{6}{7}$ | D. | 0 |
14.一组数据2、5、4、3、5、4、5的中位数和众数分别是( )
| A. | 3.5,5 | B. | 4,4 | C. | 4,5 | D. | 4.5,4 |
 画出如图所示几何体的主视图、左视图.
画出如图所示几何体的主视图、左视图.