题目内容
如图,半圆O的直径AB=4,⊙O1与半圆O内切且与AB切于点C,设⊙O1的半径为y,AC=x,
(1)请求出y关于x的函数关系式以及自变量x的取值范围;
(2)求出函数的最大值,并在所给平面直角坐标中画出函数的大致图象.
(1)请求出y关于x的函数关系式以及自变量x的取值范围;
(2)求出函数的最大值,并在所给平面直角坐标中画出函数的大致图象.

解:(1)连接OO1,连接O1C,
∴圆O1与半圆O内切,半圆O的半径为2,圆O1的半径为y,
∴OO1=2﹣y,又半圆O与AB切于点C,
O1C⊥OA,O1C=y,又AC=x,则OC=OA﹣AC=2﹣x,
在直角三角形O1OC中,根据勾股定理得:OO12=O1C2+OC2,
即(2﹣y)2=y2+(2﹣x)2,则y=﹣
 x2+x(0<x<4);
x2+x(0<x<4);(2)二次函数y=﹣
 x2+x,当x=﹣
x2+x,当x=﹣ =﹣
=﹣ =2时,
=2时,ymax=﹣
 ×22+2=1,令y=0,得到﹣
×22+2=1,令y=0,得到﹣ x2+x=0,
x2+x=0,解得:x=0或x=4,∴抛物线与x轴交于(0,0)及(4,0),
对称轴为直线x=2,作出二次函数的图象,如图所示.


练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
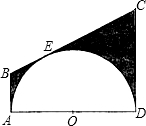 如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.
如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.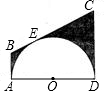 如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
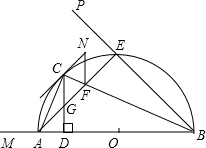 N∥CD,过C作圆的切线交FN于N.
N∥CD,过C作圆的切线交FN于N. 如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( )
如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( ) 如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.
如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.