题目内容
 如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.
如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.(1)求AP的长.
(2)求图中阴影部分的面积(结果保留π).
分析:(1)先根据题意判断出△O′PB是等腰直角三角形,由锐角三角函数的定义求出PB的长,进而可得出AP的长;
(2)根据S阴影=S扇形O′A′P′+S△O′PB直接进行计算即可.
(2)根据S阴影=S扇形O′A′P′+S△O′PB直接进行计算即可.
解答:解:(1)∵∠OBA′=45°,O′P=O′B,
∴△O′PB是等腰直角三角形,
∴PB=
BO,
∴AP=AB-BP=20-10
;
(2)阴影部分面积为:
S阴影=S扇形O′A′P′+S△O′PB=
×π×100+10×10×
=25π+50.
∴△O′PB是等腰直角三角形,
∴PB=
| 2 |
∴AP=AB-BP=20-10
| 2 |
(2)阴影部分面积为:
S阴影=S扇形O′A′P′+S△O′PB=
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查的是扇形面积的计算及图形旋转的性质,解答此题的关键是根据旋转的性质得出S阴影=S扇形O′A′P′+S△O′PB.

练习册系列答案
相关题目
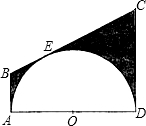 如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.
如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.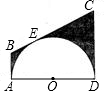 如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
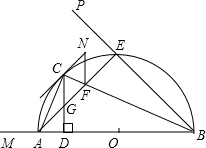 N∥CD,过C作圆的切线交FN于N.
N∥CD,过C作圆的切线交FN于N. 如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( )
如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( )