题目内容
(2013•莒南县二模)若反比例函数y=(2k-1)x3k2-2k-1的图象位于二、四象限,则k=
0
0
.分析:首先根据反比例函数定义可得3k2-2k-1=-1,解出k的值,再根据反比例函数所在象限可得2k-1<0,求出k的取值范围,然后在确定k的值即可.
解答:解:∵函数y=(2k-1)x3k2-2k-1是反比例函数,
∴3k2-2k-1=-1,
解得:k=0或
,
∵图象位于二、四象限,
∴2k-1<0,
解得:k<
,
∴k=0,
故答案为:0.
∴3k2-2k-1=-1,
解得:k=0或
| 2 |
| 3 |
∵图象位于二、四象限,
∴2k-1<0,
解得:k<
| 1 |
| 2 |
∴k=0,
故答案为:0.
点评:此题主要考查了反比例函数的定义与性质,关键是掌握反比例函数的定义,一般式y=
(k≠0)转化为y=kx-1(k≠0)的形式.
| k |
| x |

练习册系列答案
相关题目
 (2013•莒南县二模)如图,在⊙O中,OA、OB是半径,且OA⊥OB,OA=6,点C是AB上异于A、B的动点.过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE.
(2013•莒南县二模)如图,在⊙O中,OA、OB是半径,且OA⊥OB,OA=6,点C是AB上异于A、B的动点.过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE. (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: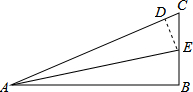 (2013•莒南县二模)如图所示的三角形纸片中,∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点D落在AC边上,折痕为AE,则BE的长为( )
(2013•莒南县二模)如图所示的三角形纸片中,∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点D落在AC边上,折痕为AE,则BE的长为( )