题目内容
 (2013•莒南县二模)如图,在⊙O中,OA、OB是半径,且OA⊥OB,OA=6,点C是AB上异于A、B的动点.过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE.
(2013•莒南县二模)如图,在⊙O中,OA、OB是半径,且OA⊥OB,OA=6,点C是AB上异于A、B的动点.过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE.(1)求证:四边形OGCH为平行四边形;
(2)①当点C在AB上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度;若不存在,请说明理由;
②求
| 1 | 3 |
分析:(1)首先证明四边形OECD是矩形,得出OG=CH,同理可证OH=CG,得出四边形OGCH为平行四边形;
(2)①根据点C是AB上的点,OA=6,得出OC=OA=6,由DG=GH=HE,得出DG=
ED=2;
②首先得出△DHF∽△DEC,进而得出
=
=
,利用DF=
CD,从而得出CF=CD-FD=
CD,再利用勾股定理得出
CD2+CH2的值.
(2)①根据点C是AB上的点,OA=6,得出OC=OA=6,由DG=GH=HE,得出DG=
| 1 |
| 3 |
②首先得出△DHF∽△DEC,进而得出
| DF |
| DC |
| DH |
| DE |
| 4 |
| 6 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答: (1)证明:如图,
(1)证明:如图,
∵CD⊥OA,CE⊥OB,
∴∠ODC=∠OEC=90°
又∵∠AOB=90°,
∴四边形OECD是矩形.
∴OD=EC,且OD∥EC,
∴∠ODG=∠CEH
∵DG=EH,
∴△ODG≌△CEH,
∴OG=CH.
同理可证OH=CG
∴四边形OGCH为平行四边形;
(2)解:①线段DG的长度不变.
∵点C是AB上的点,OA=6.
∴OC=OA=6
∵四边形OECD是矩形,
∴ED=OC=6,
∵DG=GH=HE,
∴DG=
ED=2;
②如图,过点H作HF⊥CD于点F,
∵EC⊥CD,
∴HF∥EC,
∴△DHF∽△DEC,
∴
=
=
,
∴DF=
CD,
从而CF=CD-FD=
CD
在Rt△CHF中,CH2=HF2+CF2=HF2+
CD2
在Rt△HFD中,HF2=DH2-DF2=16-
CD2,
∴CH2=16-
CD2+
CD2=16-
CD2
∴
CD2+CH2=
CD2+16-
CD2=16.
 (1)证明:如图,
(1)证明:如图,∵CD⊥OA,CE⊥OB,
∴∠ODC=∠OEC=90°
又∵∠AOB=90°,
∴四边形OECD是矩形.
∴OD=EC,且OD∥EC,
∴∠ODG=∠CEH
∵DG=EH,
∴△ODG≌△CEH,
∴OG=CH.
同理可证OH=CG
∴四边形OGCH为平行四边形;
(2)解:①线段DG的长度不变.
∵点C是AB上的点,OA=6.
∴OC=OA=6
∵四边形OECD是矩形,
∴ED=OC=6,
∵DG=GH=HE,
∴DG=
| 1 |
| 3 |
②如图,过点H作HF⊥CD于点F,
∵EC⊥CD,
∴HF∥EC,
∴△DHF∽△DEC,
∴
| DF |
| DC |
| DH |
| DE |
| 4 |
| 6 |
∴DF=
| 2 |
| 3 |
从而CF=CD-FD=
| 1 |
| 3 |
在Rt△CHF中,CH2=HF2+CF2=HF2+
| 1 |
| 9 |
在Rt△HFD中,HF2=DH2-DF2=16-
| 4 |
| 9 |
∴CH2=16-
| 4 |
| 9 |
| 1 |
| 9 |
| 1 |
| 3 |
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
点评:此题主要考查了圆的综合应用以及相似三角形的性质和勾股定理等知识,根据已知得出CH2=16-
CD2+
CD2=16-
CD2是解题关键.
| 4 |
| 9 |
| 1 |
| 9 |
| 1 |
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: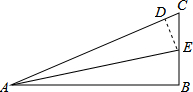 (2013•莒南县二模)如图所示的三角形纸片中,∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点D落在AC边上,折痕为AE,则BE的长为( )
(2013•莒南县二模)如图所示的三角形纸片中,∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点D落在AC边上,折痕为AE,则BE的长为( )