题目内容
阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是增函数.
例题:证明函数f(x)=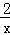 (x>0)是减函数.
(x>0)是减函数.
证明:假设x1<x2,且x1>0,x2>0
f(x1)﹣f(x2)=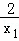 ﹣
﹣ =
=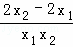 =
=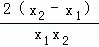
∵x1<x2,且x1>0,x2>0
∴x2﹣x1>0,x1x2>0
∴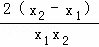 >0,即f(x1)﹣f(x2)>0
>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)=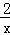 (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
(1)函数f(x)=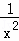 (x>0),f(1)=
(x>0),f(1)=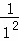 =1,f(2)=
=1,f(2)=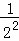 =
=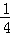 .
.
计算:f(3)= 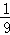 ,f(4)=
,f(4)= 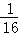 ,猜想f(x)=
,猜想f(x)=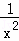 (x>0)是 减 函数(填“增”或“减”);
(x>0)是 减 函数(填“增”或“减”);
(1)解:∵f(x)=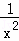 (x>0),f(1)=
(x>0),f(1)= =1,f(2)=
=1,f(2)= =
= ,
,
∴f(3)= =
= ,f(4)=
,f(4)= =
= ,
,
∵ >
> ,
,
∴猜想f(x)= (x>0)是减函数.
(x>0)是减函数.
故答案为: ,
, ,减;
,减;
(2)证明:假设x1<x2,且x1>0,x2>0
f(x1)﹣f(x2)= ﹣
﹣ =
= =
= ,
,
∵x1<x2,且x1>0,x2>0
∴x2﹣x1>0,x2+x1>0,x12 •x22>0,
•x22>0,
∴ >0,即f(x1)﹣f(x2)>0
>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)= (x>0)是减函数.
(x>0)是减函数.

练习册系列答案
相关题目

 B.
B.  C.
C.  D.
D. 
 的图象上.
的图象上. 中,自变量x的取值范围是 .
中,自变量x的取值范围是 .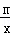 (m≠0)的一个交点.
(m≠0)的一个交点.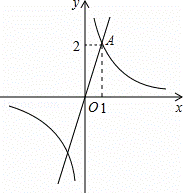
 B. 3x2 C. 2xy3 D. 2x 3
B. 3x2 C. 2xy3 D. 2x 3 .线段AB的中垂线与线段AC的中垂线的交点
.线段AB的中垂线与线段AC的中垂线的交点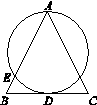 图4
图4

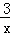 (x>0)的图象上,则△OAB的面积等于 .
(x>0)的图象上,则△OAB的面积等于 .