题目内容
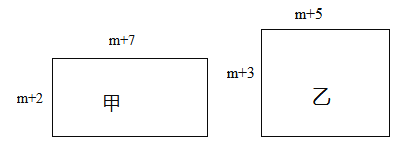
【题目】已知有甲、乙两个长方形,它们的边长如图所示(m为正整数),面积分别为S1、S2.
(1)请比较S1与S2的大小: S1 S2;
(2)若一个正方形与甲的周长相等.
①求该正方形的边长(用含m的代数式表示);
②若该正方形的面积为S3,试探究:S3与S1的差(即S3﹣S1)是否为常数?若为常数,求出这个常数;如果不是,请说明理由;
(3)若满足条件0<n<|S1﹣S2|的整数n有且只有8个,直接写出m的值并分别求出S1与S2的值.
【答案】(1)≥;(2)①m+![]() ;②S3-S1=
;②S3-S1=![]() 是一个常数 ;(3)m=10,S1=204,S2=195
是一个常数 ;(3)m=10,S1=204,S2=195
【解析】
(1)分别计算出甲,乙两长方形的面积S1、S2,利用m的取值比较为S1-S2的大小即可判断;(2)①先求出甲长方形的周长,再得出正方形的边长;②根据正方形放任边长求出S3,即可求出S3﹣S1,再进行判断;③根据S1﹣S2的取值与整数n有且只有8个,得出m的值即可,再求出S1与S2的值.
(1)S1=(m+2)(m+7)=m2+9m+14,S2=(m+3)(m+5)=m2+8m+15
故S1-S2=m-1,
∵m为正整数,故S1≥S2;
(2)∵甲的周长=2(m+2+m+7)=4m+18
∴正方形的边长为![]() =m+
=m+![]()
S1=(m+2)(m+7)=m2+9m+14
S3=(m+![]() )2=m2+9m+
)2=m2+9m+![]()
S3-S1=![]() -14=
-14=![]() ,是一个常数,是
,是一个常数,是![]()
(3)m=10
此时S1=12×17=204,S2=13×15=195

练习册系列答案
相关题目