��Ŀ����
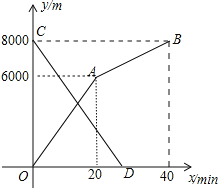
����Ŀ����ֱ������OABC�У�CB��OA����COA��90�㣬CB��3��OA��6��BA��3![]() ���ֱ���OA��OC������ֱ��Ϊx�ᡢy�Ὠ����ͼ1��ʾ��ƽ��ֱ������ϵ��
���ֱ���OA��OC������ֱ��Ϊx�ᡢy�Ὠ����ͼ1��ʾ��ƽ��ֱ������ϵ��
��1�����B�����ꣻ
��2����֪D��E�ֱ�Ϊ�߶�OC��OB�ϵĵ㣬OD��5��OE��2EB��ֱ��DE��x���ڵ�F������E��EG��x����G����EG��OG��2����ֱ��DE�Ľ���ʽ��
��3����M�ǣ�2����ֱ��DE�ϵ�һ�����㣬��x���Ϸ���ƽ�����Ƿ������һ��N��ʹ��O��D��M��NΪ������ı��������Σ������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�

���𰸡�
��1����ͼ����BH��x�ᣬ����ΪH����ô�ı���BCOHΪ���Σ�OH��CB��3��
��Rt��ABH�У�AH��3��BA��![]() ������BH��6����˵�B������Ϊ(3,6)��
������BH��6����˵�B������Ϊ(3,6)��
��2����ΪOE��2EB������![]() ��
��![]() ��E(2,4)��
��E(2,4)��
��ֱ��DE�Ľ���ʽΪy��kx��b������D(0,5)��E(2,4)��
��![]() ���
���![]() ��
��![]() ������ֱ��DE�Ľ���ʽΪ
������ֱ��DE�Ľ���ʽΪ![]() ��
��
��3����![]() ��ֱ֪��DE��x�ύ�ڵ�F(10,0)��OF��10��DF��
��ֱ֪��DE��x�ύ�ڵ�F(10,0)��OF��10��DF��![]() ��
��
����ͼ����DOΪ���εĶԽ���ʱ��MN��DO���ഹֱƽ�֣���M��DF���е㣮
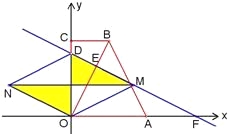
��ʱ��M������Ϊ(5,![]() )����N������Ϊ(��5,
)����N������Ϊ(��5,![]() )��
)��
����ͼ����DO��DNΪ���ε��ڱ�ʱ����N���O���ڵ�E�Գƣ���ʱ��N������Ϊ(4,8)��
����ͼ����DO��DMΪ���ε��ڱ�ʱ��NO��5���ӳ�MN��x����P��
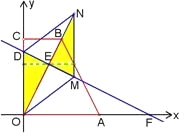
����NPO�ס�DOF����![]() ��
��
��![]() ��
��
���![]() ��
��![]() ����ʱ��N������Ϊ
����ʱ��N������Ϊ![]() ��
��
��������
��1����BH��x�ᣬ�������Σ���ֱ�������������BH=6���Ӷ���õ�B������Ϊ(3,6)��
��2������ϵ�������ֱ�߽���ʽ��
��3���ۺ��Խ�ǿ������ȫ������ȷ����Ĺؼ���

 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y+2����y+6��+4 ����һ����
=y2+8y+16 ���ڶ�����
=��y+4��2����������
=��x2��4x+4��2�����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_______��
A����ȡ����ʽ |
B��ƽ���ʽ |
C�������͵���ȫƽ����ʽ |
D�����������ȫƽ����ʽ |
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿף�________�����������������������������������ף���ֱ��д����ʽ�ֽ�������_________ ��
��3������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮