题目内容
如图9,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),抛物线上另有一点
的左侧),抛物线上另有一点![]() 在第一象限,满足∠
在第一象限,满足∠![]() 为直角,且恰使△
为直角,且恰使△![]() ∽△
∽△![]() .
.

(1)(3分)求线段![]() 的长.
的长.
(2)(3分)求该抛物线的函数关系式.
(3)(4分)在![]() 轴上是否存在点
轴上是否存在点![]() ,使△
,使△![]() 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
(1)2![]()
(2)y=-![]() x
x![]() +
+![]() x-4
x-4![]()
(3)(0,0),(6-2![]() ,0),(4,0),(6+2
,0),(4,0),(6+2![]() ,0)
,0)
解析:(1)解:由ax![]() -8ax+12a=0(a<0)得
-8ax+12a=0(a<0)得
![]() x
x![]() =2,x
=2,x![]() =6
=6
即:OA=2,OB=6 ……1分
∵△OCA∽△OBC
∴OC![]() =OA·OB=2×6 ……2分
=OA·OB=2×6 ……2分
∴OC=2![]() (-2
(-2![]() 舍去)
舍去)
∴线段OC的长为2![]() ……3分
……3分
(2)解:∵△OCA∽△OBC
 ∴
∴![]()
设AC=k,则BC=![]() k
k
由AC![]() +BC
+BC![]() =AB
=AB![]() 得
得
k![]() +(
+(![]() k)
k)![]() =(6-2)
=(6-2)![]()
解得k=2(-2舍去)
∴AC=2,BC=2![]() =OC ……1分
=OC ……1分
过点C作CD⊥AB于点D
∴OD=![]() OB=3
OB=3
∴CD=![]()
∴C的坐标为(3,![]() ) ……2分
) ……2分
将C点的坐标代入抛物线的解析式得
 =a(3-2)(3-6)
=a(3-2)(3-6)
∴a=-![]()
∴抛物线的函数关系式为:
y=-![]() x
x![]() +
+![]() x-4
x-4![]() ……3分
……3分
(3)解:①当P![]() 与O重合时,△BCP
与O重合时,△BCP![]() 为等腰三角形
为等腰三角形
∴P![]() 的坐标为(0,0) ……1分
的坐标为(0,0) ……1分
②当P![]() B=BC时(P
B=BC时(P![]() 在B点的左侧),△BCP
在B点的左侧),△BCP 为等腰三角形
为等腰三角形
∴P![]() 的坐标为(6-2
的坐标为(6-2![]() ,0) ……2分
,0) ……2分
③当P![]() 为AB的中点时,P
为AB的中点时,P![]() B=P
B=P![]() C,△BCP
C,△BCP![]() 为等腰三角形
为等腰三角形
∴P![]() 的坐标为(4,0) ……3分
的坐标为(4,0) ……3分
④![]() 当BP
当BP![]() =BC时(P
=BC时(P![]() 在B点的右侧),△BCP
在B点的右侧),△BCP 为等腰三角形
为等腰三角形
∴P![]() 的坐标为(6+2
的坐标为(6+2![]() ,0)
,0)
∴在x轴上存在点P,使△BCP为等腰三角形,符合条件的点P的坐标为:
(0,0),(6-2![]() ,0),(4,0),(6+2
,0),(4,0),(6+2 ,0) ……4分
,0) ……4分


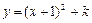 与
与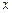 轴交于A、B两点,与
轴交于A、B两点,与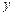 轴交于点C(0,
轴交于点C(0,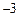 ).
).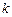 的值;
的值;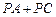 的值最小,求此时点P的坐标;
的值最小,求此时点P的坐标;
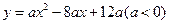 与
与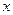 轴交于
轴交于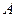 、
、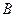 两点(点
两点(点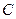 在第一象限,满足∠
在第一象限,满足∠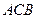 为直角,且恰使△
为直角,且恰使△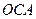 ∽△
∽△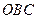 .
.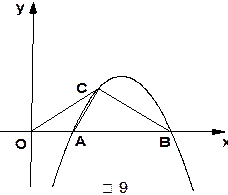
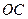 的长.
的长. 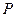 ,使△
,使△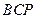 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的 与
与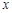 轴交于A、B两点,与
轴交于A、B两点,与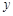 轴交于点C(0,
轴交于点C(0,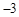 ).
).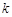 的值;
的值;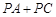 的值最小,求此时点P的坐标;
的值最小,求此时点P的坐标;
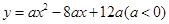 与
与 轴交于
轴交于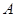 、
、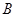 两点(点
两点(点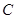 在第一象限,满足∠
在第一象限,满足∠ 为直角,且恰使△
为直角,且恰使△ ∽△
∽△ .
.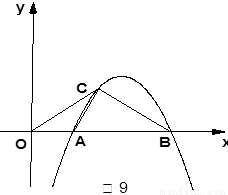
 的长.
的长. 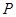 ,使△
,使△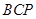 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的