题目内容
 如图,直线y=
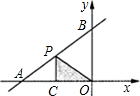
如图,直线y=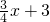 与x轴、y轴交于A、B两点,点P是直线AB上的点,它的横坐标为a(-4<a<0),PC⊥x轴于点C,设△POC的面积为S,则S的大小范围为________.
与x轴、y轴交于A、B两点,点P是直线AB上的点,它的横坐标为a(-4<a<0),PC⊥x轴于点C,设△POC的面积为S,则S的大小范围为________.
0<S≤1.5
分析:求出直线和x轴的交点坐标,将C点横坐标代入解析式,求出P点的纵坐标,根据三角形的面积公式求出S的表达式---为关于a的二次函数,求出二次函数的最大值即为S的最大值,从图可知,S的最小值为0.
解答:∵P的横坐标为a,
将x=a代入解析式y=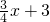 得,
得,
y= ,
,
S= (-a)(
(-a)( a+3)=-
a+3)=- (a+2)2+
(a+2)2+ ,
,
当a=-2时,S取得最大值: ;
;
由图可知,S取的最小值:0.
可见,0<S≤1.5.
故答案为0<S≤1.5.
点评:本题考查了一次函数和三角形及二次函数的关系,将三角形的最值问题通过一次函数转化为二次函数最值是解题的关键.
分析:求出直线和x轴的交点坐标,将C点横坐标代入解析式,求出P点的纵坐标,根据三角形的面积公式求出S的表达式---为关于a的二次函数,求出二次函数的最大值即为S的最大值,从图可知,S的最小值为0.
解答:∵P的横坐标为a,
将x=a代入解析式y=
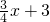 得,
得,y=
 ,
,S=
 (-a)(
(-a)( a+3)=-
a+3)=- (a+2)2+
(a+2)2+ ,
,当a=-2时,S取得最大值:
 ;
;由图可知,S取的最小值:0.
可见,0<S≤1.5.
故答案为0<S≤1.5.
点评:本题考查了一次函数和三角形及二次函数的关系,将三角形的最值问题通过一次函数转化为二次函数最值是解题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
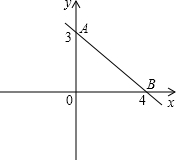 如图,直线m与x轴、y轴分别交于点B,A,且A,B两点的坐标分别为A(0,3),B(4,0).
如图,直线m与x轴、y轴分别交于点B,A,且A,B两点的坐标分别为A(0,3),B(4,0).

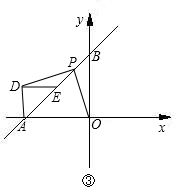
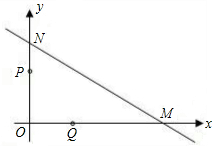 点同时停止运动,设运动时间为t秒.
点同时停止运动,设运动时间为t秒. 已知:如图,直线AB与x轴交于点A,与y轴交于点B.
已知:如图,直线AB与x轴交于点A,与y轴交于点B.