题目内容
16.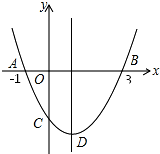 抛物线y=ax2+bx+c交x轴于A(-1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:
抛物线y=ax2+bx+c交x轴于A(-1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=$\frac{1}{2}$;⑤当△ABC是等腰三角形时,a的值有3个.
其中正确的有( )
| A. | ①③④ | B. | ①②④ | C. | ①③⑤ | D. | ③④⑤ |
分析 根据二次函数图象与系数的关系,二次函数与x轴交于点A(-1,0)、B(3,0),可知二次函数的对称轴为x=$\frac{(-1)+3}{2}$=1,即$-\frac{b}{2a}=1$,可得2a与b的关系;将A、B两点代入可得c、b的关系;函数开口向下,x=1时取得最小值,则m≠1,可判断③;根据图象AD=BD,顶点坐标,判断④;由图象知BC≠AC,从而可以判断⑤.
解答 解:∵二次函数与x轴交于点A(-1,0)、B(3,0).
∴二次函数的对称轴为x=$\frac{(-1)+3}{2}$=1,即$-\frac{b}{2a}=1$.
∴b=-2a.
∴2a+b=0.(故①正确)
∵二次函数y=ax2+bx+c与x轴交于点A(-1,0)、B(3,0).
∴a-b+c=0,9a+3b+c=0.
又∵b=-2a.
∴3b=-6a,a-(-2a)+c=0.
∴3b=-6a,2c=-6a.
∴2c=3b.(故②错误)
∵抛物线开口向上,对称轴是x=1.
∴x=1时,二次函数有最小值.
∴m≠1时,a+b+c<am2+bm+c.
即a+b<am2+bm.(故③正确)
∵AD=BD,AB=4,△ABD是等腰直角三角形.
∴AD2+BD2=42.
解得,AD2=8.
设点D坐标为(1,y).
则[1-(-1)]2+y2=AD2.
解得y=±2.
∵点D在x轴下方.
∴点D为(1,-2).
∵二次函数的顶点D为(1,-2),过点A(-1,0).
设二次函数解析式为y=a(x-1)2-2.
∴0=a(-1-1)2-2.
解得a=$\frac{1}{2}$.(故④正确)
由图象可得,AC≠BC.
故△ABC是等腰三角形时,a的值有2个.(故⑤错误)
故①③④正确,②⑤错误.
故选项A正确,选项B错误,选项C错误,选项D错误.
故选A.
点评 本题考查二次函数图象与系数的关系,关键是找出图象中和题目中的有关信息,来判断问题中结论是否正确.

 阅读快车系列答案
阅读快车系列答案| A. | 130000 | B. | 1.3×105 | C. | 1.3×106 | D. | 1.3×107 |
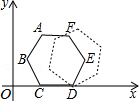 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,最先会过点(2015,2)的是( )
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,最先会过点(2015,2)的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
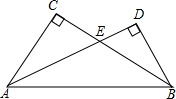 如图,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,AD与BC相交于点E,则∠CAE与∠DBE的大小关系是( )
如图,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,AD与BC相交于点E,则∠CAE与∠DBE的大小关系是( )| A. | ∠CAE>∠DBE | B. | ∠CAE=∠DBE | C. | ∠CAE<∠DBE | D. | 无法确定 |
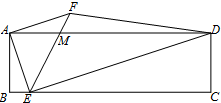 如图,矩形ABCD中,E为BC边上一点,且AE⊥DE.将线段AE绕A点逆时针旋转90°,得到线段AF.连接EF,交AD于点M,连接DF.若BE=1,EF=2$\sqrt{5}$,则点M到DF的距离为$\frac{3}{4}$$\sqrt{2}$.
如图,矩形ABCD中,E为BC边上一点,且AE⊥DE.将线段AE绕A点逆时针旋转90°,得到线段AF.连接EF,交AD于点M,连接DF.若BE=1,EF=2$\sqrt{5}$,则点M到DF的距离为$\frac{3}{4}$$\sqrt{2}$.