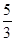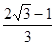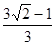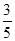题目内容
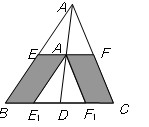
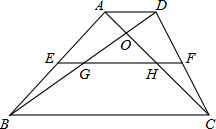
如图,在梯形ABCD中,AD∥BC,E、F分别是AB、CD的中点,则下列结论:①EF∥AD; ②S△ABO=S△DCO;③△OGH是等腰三角形;④BG=DG;⑤EG=HF。其中正确的个数是【 】
A、1个 B、2个 C、3个 D、4个

A、1个 B、2个 C、3个 D、4个
D
梯形中位线定理,等腰三角形的判定,三角形中位线定理。
【分析】∵在梯形ABCD中,AD∥BC,E、F分别是AB、CD的中点,
∴EF∥AD∥BC,∴①正确。
∵在梯形ABCD中,△ABC和△DBC是同底等高的三角形,
∴S△ABC=S△DBC。∴S△AB C-S△OBC =S△DBC-S△OBC,即S△ABO=S△DCO。∴②正确。
∵EF∥BC,∴∠OGH=∠OBC,∠OHG=∠OCB。
已知四边形ABCD是梯形,不一定是等腰梯形,即∠OBC和∠OCB不一定相等,
即∠OGH和∠OHG不一定相等,∠GOH和∠OGH或∠OHG也不能证出相等。
∴△OGH是等腰三角形不对,∴③错误。
∵EF∥BC,AE=BE(E为AB中点),∴BG=DG,∴④正确。
∵EF∥BC,AE=BE(E为AB中点),∴AH=CH。
∵E、F分别为AB、CD的中点,∴EH=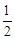 BC,FG=
BC,FG=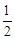 BC。∴EH=FG。
BC。∴EH=FG。
∴EG=FH,∴⑤正确。
∴正确的个数是4个。故选D。
【分析】∵在梯形ABCD中,AD∥BC,E、F分别是AB、CD的中点,
∴EF∥AD∥BC,∴①正确。
∵在梯形ABCD中,△ABC和△DBC是同底等高的三角形,
∴S△ABC=S△DBC。∴S△AB C-S△OBC =S△DBC-S△OBC,即S△ABO=S△DCO。∴②正确。
∵EF∥BC,∴∠OGH=∠OBC,∠OHG=∠OCB。
已知四边形ABCD是梯形,不一定是等腰梯形,即∠OBC和∠OCB不一定相等,
即∠OGH和∠OHG不一定相等,∠GOH和∠OGH或∠OHG也不能证出相等。
∴△OGH是等腰三角形不对,∴③错误。
∵EF∥BC,AE=BE(E为AB中点),∴BG=DG,∴④正确。
∵EF∥BC,AE=BE(E为AB中点),∴AH=CH。
∵E、F分别为AB、CD的中点,∴EH=
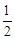 BC,FG=
BC,FG=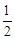 BC。∴EH=FG。
BC。∴EH=FG。∴EG=FH,∴⑤正确。
∴正确的个数是4个。故选D。

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目


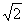 ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号) 分别是△
分别是△ 的边
的边 上的点,若
上的点,若 ,
, ,
, .
.
 ∽△
∽△ ,求
,求 的长.
的长. AB,DF∥BC,E为BD的中点.若EF⊥AC,BC=6,则四边形DBCF的面积为 ▲ .
AB,DF∥BC,E为BD的中点.若EF⊥AC,BC=6,则四边形DBCF的面积为 ▲ .