题目内容
图5是一个长为400米的环形跑道,其中A、B为跑道对称轴上的两点,且A、B之间有一条50米的直线通道。甲、乙两人同时从A点出发,甲按逆时针方向以速度v1沿跑道跑步,当跑到B点处时继续沿跑道前进,乙按顺时针方向以速度v2沿跑道跑步,当跑到B点处时沿直线通道跑回A点处。假设两人跑步时间足够长。求:
⑴如果v1∶v2=3∶2,那么甲跑了多少路程后,两人首次在A点处相遇?
⑵如果v1∶v2=5∶6,那么乙跑了多少路程后,两人首次在B点处相遇?
 |
⑴设甲跑了n圈后,两人首次在A点处相遇,再设甲、乙两人的速度分别为v1=3m,v2=2m,
由题意可得在A处相遇时,他们跑步的时间是![]() (2分)
(2分)
是![]() (3分)
(3分)
因为乙跑回到A点处,所以![]() 应是250的整数倍,从而知n的最小值是15,(4分)
应是250的整数倍,从而知n的最小值是15,(4分)
所以甲跑了15圈后,两人首次在A点处相遇 ![]() (5分)
(5分)
⑵设乙跑了![]() 米,甲跑了
米,甲跑了![]() 米时,两人首次在B点处相遇,设甲、乙两人的速度分别为v1=5m,v2=6m,由题意可得
米时,两人首次在B点处相遇,设甲、乙两人的速度分别为v1=5m,v2=6m,由题意可得![]() ,即
,即![]() , (7分)
, (7分)
所以![]() ,即
,即![]() (p,q均为正整数)。
(p,q均为正整数)。
所以p,q的最小值为q=2,p=4, (8分)
此时,乙跑过的路程为250×4+200=1200(米)。 ![]() (9分)
(9分)
所以乙跑了1200米后,两人首次在B点处相遇。 (10分)

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 ,请说明理由.
,请说明理由. 前进,乙按顺时针方向以速度v2沿跑道跑步,当跑到B点处时沿直线通道跑回A点处.假设两人跑步时间足够长.求:
前进,乙按顺时针方向以速度v2沿跑道跑步,当跑到B点处时沿直线通道跑回A点处.假设两人跑步时间足够长.求: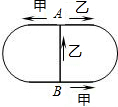 前进,乙按顺时针方向以速度v2沿跑道跑步,当跑到B点处时沿直线通道跑回A点处.假设两人跑步时间足够长.求:
前进,乙按顺时针方向以速度v2沿跑道跑步,当跑到B点处时沿直线通道跑回A点处.假设两人跑步时间足够长.求: