题目内容
如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED.

【考点】相似三角形的应用.
【分析】作AH⊥ED交FC于点G;把实际问题抽象到相似三角形中,利用相似三角形的对应边成比例列出方程,解方程即可.
【解答】解:作AH⊥ED交FC于点G;如图所示:
∵FC⊥BD,ED⊥BD,AH⊥ED交FC于点G,
∴FG∥EH,
∵AH⊥ED,BD⊥ED,AB⊥BC,ED⊥BC,
∴AH=BD,AG=BC,
∵AB=1.6,FC=2.2,BC=1,CD=5,
∴FG=2.2﹣1.6=0.6,BD=6,
∵FG∥EH,
∴ ,
,
解得:EH=3.6,
∴ED=3.6+1.6=5.2(m)
答:电视塔的高ED是5.2米.

【点评】本题考查了相似三角形的应用;通过构造相似三角形.利用相似三角形对应边成比例是解决问题的关键.

如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:
①∠AED=∠B,②∠ADE=∠C,③ ,④
,④ ,⑤
,⑤ ,
,
使△ADE与△ACB一定相似的有
| A. | ①②④ | B. | ②④⑤ | C. | ①②③④ | D. | ①②③⑤ |
| |||

有这样一个问题:探究函数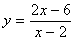 的图象与性质.
的图象与性质.
小慧根据学习函数的经验,对函数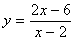 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小慧的探究过程,请补充完成:
(1)函数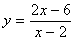 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2)列出y与x的几组对应值.请直接写出m的值,m=__________;
| x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
| y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
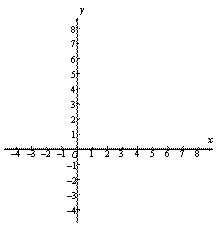
(3)请在平面直角坐标系 中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
① ;
 |
② .
 的倒数是 ,相反数是 .
的倒数是 ,相反数是 . (2
(2 =
= ,
, =
= ,则向量
,则向量 关于
关于