题目内容
 如图所示,AB∥CD,BE∥FD,则∠B+∠D=
如图所示,AB∥CD,BE∥FD,则∠B+∠D=
- A.270°
- B.180°
- C.120°
- D.150°
B
分析:根据两直线平行,内错角相等的性质得到∠B=∠BGD,又BE∥FD,所以∠BGD+∠D=180°,即∠B+∠D=180°.
解答:∵AB∥CD,
∴∠B=∠BGD(两直线平行,内错角相等),
∵BE∥FD,
∴∠BGD+∠D=180°(两直线平行,同旁内角互补),
∴∠B+∠D=180°.
故选B.
点评:本题主要考查平行线的性质,熟练掌握性质定理是解题的关键.
分析:根据两直线平行,内错角相等的性质得到∠B=∠BGD,又BE∥FD,所以∠BGD+∠D=180°,即∠B+∠D=180°.
解答:∵AB∥CD,
∴∠B=∠BGD(两直线平行,内错角相等),
∵BE∥FD,
∴∠BGD+∠D=180°(两直线平行,同旁内角互补),
∴∠B+∠D=180°.
故选B.
点评:本题主要考查平行线的性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
 5、如图所示,AB∥CD,则∠1+∠2+∠3=( )
5、如图所示,AB∥CD,则∠1+∠2+∠3=( )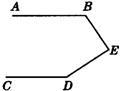 24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=
24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=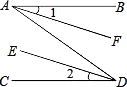 如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?
如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?
 如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=
如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=