Question

【题目】【问题学习】小芸在小组学习时问小娟这样一个问题：已知α为锐角，且sinα= ，求sin2α的值．小娟是这样给小芸讲解的：

构造如图1所示的图形，在⊙O中，AB是直径，点C在⊙O上，所以∠ACB=90°，作CD⊥AB于D．设∠BAC=α，则sinα= ，可设BC=x，则AB=3x，…．

【问题解决】

（1）请按照小娟的思路，利用图1求出sin2α的值；（写出完整的解答过程）

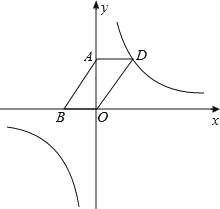
（2）如图2，已知点M，N，P为⊙O上的三点，且∠P=β，sinβ= ，求sin2β的值．

Answer 1

【答案】（1）sin2α=；（2）sin2β=sin∠MON=．

【解析】

试题分析：（1）如图1中，⊙O中，AB是直径，点C在⊙O上，所以∠ACB=90°，作CD⊥AB于D．设∠BAC=α，则sinα= ，可设BC=x，则AB=3x．利用面积法求出CD，在Rt△COD中，根据sin2α= ，计算即可．（2）如图2中，连接NO，并延长交⊙O于点Q，连接MQ，MO，过点M作MR⊥NO于点R．首先证明∠MON=2∠Q=2β，在Rt△QMN中，由sinβ=，设MN=3k，则NQ=5k，易得OM=NQ= ，可得MQ==4k，由MNMQ=NQMR，求出在Rt△MRO中，根据sin2β=sin∠MON=，计算即可．

试题解析：（1）如图1中，⊙O中，AB是直径，点C在⊙O上，所以∠ACB=90°，作CD⊥AB于D．设∠BAC=α，则sinα=，可设BC=x，则AB=3x．

∴AC== =2x，

∵ACBC=ABCD，

∴CD= x，

∵OA=OC，

∴∠OAC=∠OCA=α，

∴∠COB=2α，

∴sin2α== ．

（2）如图2中，连接NO，并延长交⊙O于点Q，连接MQ，MO，过点M作MR⊥NO于点R．

在⊙O中，∠NMQ=90°，

∵∠Q=∠P=β，∴∠MON=2∠Q=2β，

在Rt△QMN中，∵sinβ=，

∴设MN=3k，则NQ=5k，易得OM=NQ=，

∴MQ==4k，

∵ ，

∴3k4k=5kMR

∴MR= ，

在Rt△MRO中，sin2β=sin∠MON=．