Question

（1997•山东）已知A为抛物线y=

3

x2-2

3

x+

3

的顶点，B为该抛物线与y轴的交点，C为x轴上一点．设线段BC、AC、AB的长度分别为a、b、c，当a+c=2b时，求：
（1）经过B、C两点的直线的解析式；
（2）三角形ABC的面积．

Answer 1

分析：（1）首先求出二次函数的顶点坐标以及图象与y轴交点坐标，进而假设出C点位置，利用C点可能在A点右侧或左侧分别求出C点坐标即可；
（2）根据（1）中所求得出三角形ABC的面积即可．

解答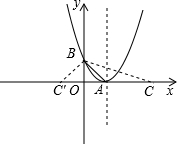：解：（1）∵y=

3

x2-2

3

x+

3

=

3

（x-1）²，
∴A点坐标为：（1，0），
∵B为该抛物线与y轴的交点，
∴x=0时，y=

3

，即B点坐标为：（0，

3

），
当C点在A点右侧，设C点坐标为：（x，0），
则AC=x-1，AB=

BO2+AO2

=2，BC=

3+x2

，
∵a+c=2b，
∴2（x-1）=2+

3+x2

，
整理得出：3x²-16x+13=0，
解得：x₁=

13

3

，x₂=1（此时A，C重合不合题意舍去），
如图所示：
当C′点在A点左侧，设C′点坐标为：（z，0），
则AC′=1-z，AB=

BO2+AO2

=2，BC′=

3+z2

，
∵a+c=2b，
∴2（1-z）=2+

3+z2

，
整理得出：3z²=3，
解得：x₁=-1，x₂=1（此时A，C重合不合题意舍去），
∴C点坐标为：（-1，0）或（

13

3

，0），
∴当B点坐标为：（0，

3

），
C点坐标为：（-1，0），
带入解析式y=kx+b，

b= 3 -k+b=0

，
解得：

b= 3 k= 3

，
∴经过B、C两点的直线的解析式为：y=

3

x+

3

，
∴当B点坐标为：（0，

3

），
C点坐标为：（

13

3

，0），
带入解析式y=ax+c，

c= 3 13 3 a+c=0

解得：

c= 3 a=- 3 3 13

，
∴经过B、C两点的直线的解析式为：y=-

3 13

13

x+

3

；

（2）∵当B点坐标为：（0，

3

），C点坐标为：（-1，0）时，
∴AC′=2，∴S_△ABC=

1

2

BO×AC′=

1

2

×2×

3

=

3

，
当B点坐标为：（0，

3

），C点坐标为：（

13

3

，0）时，
∴AC=

13

3

-1=

10

3

，
∴S_△ABC=

1

2

BO×AC=

1

2

×

3

×

10

3

=

5 3

3

．

点评：此题主要考查了二次函数的综合应用以及三角形面积求法等知识，根据分类讨论的思想得出C点坐标是解题关键．