题目内容
（1997•山东）如图，已知A是⊙O上一点，以A为圆心作圆交⊙O于B、C两点，E是弦BC上一点，连接AE并延长⊙O于D，连接BD、CD．设∠BDC=2α．（1）求证：BD•CD=AD•ED；
（2）若ED：AD=
| 3 |
| 4 |
| DB |
| AD |
| CD |
| AD |
| BD |
| CD |
分析：（1）如图，连接AB、AC．通过证明△DBA∽△DEC，得到对应边成比例，即BD：DE=AD：CD，所以BD•CD=AD•ED；
（2）如图，过点A作AF⊥BC于点F．则F为BC的中点．通过△ABE∽△ADB的对应边成比例得到
=
．通过△AEC∽△ACD的对应边成比例得到
=
，然后求得以
和
为根的一元二次方程两根之和和两根之积分别是
+
=2cosα，
•
=
=
=
cos2α，所以该方程为x2-2cosα•x+
cos2α=0．解得，x1=
cosα，x2=
cosα．需要分类讨论：当BD＜CD时，
=
=
=
；当BD＞CD时，
=
=
=3．
（2）如图，过点A作AF⊥BC于点F．则F为BC的中点．通过△ABE∽△ADB的对应边成比例得到
| BD |
| AD |
| BE |
| AB |
| CD |
| AD |
| EC |
| AC |
| DB |
| AD |
| CD |
| AD |
| BD |
| AD |
| CD |
| AD |
| BD |
| AD |
| CD |
| AD |
| AD•ED |
| AD2 |
| ED |
| AD |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| BD |
| CD |
| ||
|
| x1 |
| x2 |
| 1 |
| 3 |
| BD |
| CD |
| ||
|
| x2 |
| x1 |
解答：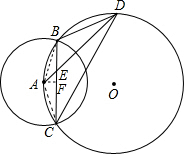
（1）证明：如图，连接AB、AC．
∵A是⊙O上一点，以A为圆心作圆交⊙O于B、C两点，
∴AB=AC，
=
，
∴∠ADB=∠ADC，．
又∵∠BAD=∠BCD，
∴△DBA∽△DEC，
∴BD：DE=AD：CD，
∴BD•CD=AD•ED；
（2）如图，过点A作AF⊥BC于点F．则F为BC的中点．
∵∠BDC=2α．
∴∠ACB=∠ABC=α，则FC=AC•cosα，
∴BC=2FC=2AC•cosα．
∵∠ABE=∠ADB，∠BAD=∠BAE，
∴△ABE∽△ADB，
∴
=
．
同理，△AEC∽△ACD，则
=
，
∴
+
=
+
=
=
=2cosα．
又由（1）知，BD•CD=AD•ED，
∴
•
=
=
=
cos2α，
∴以
和
为根的一元二次方程为x2-2cosα•x+
cos2α=0．
解得，x1=
cosα，x2=
cosα．
当BD＜CD时，
=
=
=
；
当BD＞CD时，
=
=
=3．
（1）证明：如图，连接AB、AC．∵A是⊙O上一点，以A为圆心作圆交⊙O于B、C两点，
∴AB=AC，
 |
| AC |
|
| AB |
∴∠ADB=∠ADC，．
又∵∠BAD=∠BCD，
∴△DBA∽△DEC，
∴BD：DE=AD：CD，
∴BD•CD=AD•ED；
（2）如图，过点A作AF⊥BC于点F．则F为BC的中点．
∵∠BDC=2α．
∴∠ACB=∠ABC=α，则FC=AC•cosα，
∴BC=2FC=2AC•cosα．
∵∠ABE=∠ADB，∠BAD=∠BAE，
∴△ABE∽△ADB，
∴
| BD |
| AD |
| BE |
| AB |
同理，△AEC∽△ACD，则
| CD |
| AD |
| EC |
| AC |
∴
| BD |
| AD |
| CD |
| AD |
| BE |
| AB |
| EC |
| AC |
| BE+EC |
| AC |
| BC |
| AC |
又由（1）知，BD•CD=AD•ED，
∴
| BD |
| AD |
| CD |
| AD |
| AD•ED |
| AD2 |
| ED |
| AD |
| 3 |
| 4 |
∴以
| DB |
| AD |
| CD |
| AD |
| 3 |
| 4 |
解得，x1=
| 1 |
| 2 |
| 3 |
| 2 |
当BD＜CD时，
| BD |
| CD |
| ||
|
| x1 |
| x2 |
| 1 |
| 3 |
当BD＞CD时，
| BD |
| CD |
| ||
|
| x2 |
| x1 |
点评：本题综合考查了相交两圆的性质，垂径定理，相似三角形的判定与性质以及一元二次方程等知识点．难度比较大．
练习册系列答案
口算能手系列答案
相关题目
（1997•山东）如图，ABCD是一个正方形，P、Q是正方形外两点，且△APD和△BCQ是等边三角形，则∠PQD的正切值是（ ）
（1997•山东）如图，AB是⊙O的弦，C是弦AB上一点，且BC：CA=2：1，连接OC并延长交⊙O于D，若DC=2cm，OC=3cm，则圆心O到弦AB的距离为（ ）
（1997•山东）如图，在△ABC中，∠B=22.5°，边AB的垂直平分线交BC于D，DF⊥AC于F，并与BC边上的高AE交于G．求证：EG=EC．