题目内容
已知：如图，E，B，F，C四点在同一直线上，∠A=∠D=90°，BE=FC，AB=DF．求证：∠E=∠C．
证明：∵BE=FC，
∴BE+BF=FC+BF，即EF=BC，
∵∠A=∠D=90°，
在RT△ABC和RT△DFE中，
，
∴△ABC≌△DFE（HL），
∴∠E=∠C．
分析：先得出BE=FC，由HL可得△ABC≌△DFE，进而可得出结论．
点评：本题主要考查了全等三角形的判定及性质，应熟练掌握．
∴BE+BF=FC+BF，即EF=BC，
∵∠A=∠D=90°，
在RT△ABC和RT△DFE中，
，∴△ABC≌△DFE（HL），
∴∠E=∠C．
分析：先得出BE=FC，由HL可得△ABC≌△DFE，进而可得出结论．
点评：本题主要考查了全等三角形的判定及性质，应熟练掌握．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，测得C在B的北偏西45°方向上．
11、已知，如图，正比例函数与反比例函数的图象相交于A、B两点，A点坐标为（2，1），分别以A、B为圆心的圆与x轴相切，则图中两个阴影部分面积的和为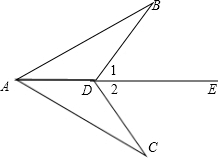
已知，如图，∠1=∠2，
已知，如图，直角坐标系内的矩形ABCD，顶点A的坐标为（0，3），BC=2AB，P为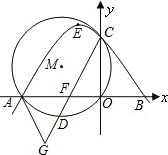
于C点，⊙M经过原点O及点A、C，点D是劣弧