Question

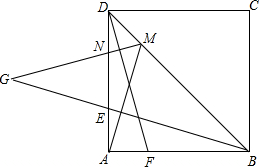（2007•甘井子区模拟）如图，正方形ABCD中，若E、F分别是AD、AB上的点，且AE=AF．过点A作AM⊥BE，交对角线BD于M，过点M作MG⊥DF，交AD于N，交BE的延长线于G．探究BG、AM、MG之间的数量关系并证明．

Answer 1

分析：连接MC，首先根据题干条件结合正方形的性质证明△ABM≌△CBM，得出AM=CM，∠AMB=∠CMB，∠MCB=∠MAB，再证明△ABE≌△ADF，得到∠ABE=∠ADF，结合AM⊥BE，MG⊥DF，得到∠DMG=∠AMB=∠CMB，于是可以证明C，M，G三点在同一直线上，综合以上条件可以证明结论．

解答：答：BG，AM，MG之间的数量关系是：BG=AM+MG．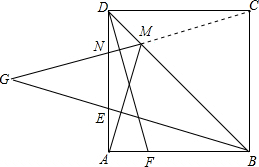
证明：连结MC．
∵ABCD是正方形，
∴AB=AD=BC=CD，∠ADB=∠ABD=∠CBD=45°，
∵在△ABM与△CBM中，

AB=BC ∠ABD=∠CBD BM=BM

，
∴△ABM≌△CBM（SAS），
∴AM=CM，∠AMB=∠CMB，∠MCB=∠MAB，
∵在△ABE与△ADF中，

AE=AF AB=AD ∠BAE=∠DAF

，
∴△ABE≌△ADF（SAS），
∴∠ABE=∠ADF，
又∵∠ABD=∠ADB=45度，
∴∠EBD=∠FDB，
∵AM⊥BE，MG⊥DF，
∴∠EBD+∠AMB=∠FDB+∠DMG=90°，
∴∠DMG=∠AMB=∠CMB，
∴C，M，G三点在同一直线上，
∴CG=CM+MG，
∵∠MAB+∠ABE=∠GBC+∠ABE=90°，
∴∠MAB=∠GBC，
∵∠MAB=∠MCB
∴∠GBC=∠MCB，
∴BG=CG=CM+MG．

点评：本题主要考查正方形的性质等知识点，解答本题的关键是熟练掌握正方形的性质以及全等三角形的判定定理，此题涉及角之间的等量关系较多，希望引起同学的注意．