Question

4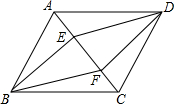．如图，在□ABCD中，E、F是对角线AC上的两点，AE=CF．
（1）求证：四边形BEDF是平行四边形；
（2）联结BD交EF于点O，当BE⊥EF时，BE=8，BF=10，求BD的长．

Answer 1

分析 （1）连接BD交AC于O．只要证明OE=OF，OB=OD即可．
（2）在Rt△BEF中，EF=$\sqrt{B{F}^{2}-B{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，推出OE=OF=3，在Rt△BEO中，OB=$\sqrt{B{E}^{2}+O{E}^{2}}$=$\sqrt{{8}^{2}+{3}^{2}}$=$\sqrt{73}$，由此即可解决问题．

解答 （1）证明：连接BD交AC于O．
∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵AE=CF，
∴OE=OF，∵OB=OD，
∴四边形BEDF是平行四边形；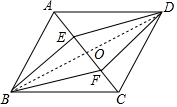

（2）解：∵BE⊥AC，
∴∠BEF=90°，
在Rt△BEF中，EF=$\sqrt{B{F}^{2}-B{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∴OE=OF=3，
在Rt△BEO中，OB=$\sqrt{B{E}^{2}+O{E}^{2}}$=$\sqrt{{8}^{2}+{3}^{2}}$=$\sqrt{73}$，
∴BD=2OB=2$\sqrt{73}$．

点评 本题考查平行四边形的判定和性质、勾股定理等知识，解题的关键是熟练掌握平行四边形的判定和性质，灵活运用勾股定理解决问题吗，属于中考常考题型．