题目内容
以下题目的解答正确吗?若不正确,请改正.
已知x+y=-3,xy=2,求
+
.
解:∵x+y=-3,xy=2,∴原式=
+
=
=
=
=-
.
已知x+y=-3,xy=2,求
|
|
解:∵x+y=-3,xy=2,∴原式=
| ||
|
| ||
|
(
| ||||
|
| x+y | ||
|
| -3 | ||
|
| 3 |
| 2 |
| 2 |
分析:根据实数的性质得到x<0,y<0,则根据二次根式的性质把原式化简为原式=-
-
,然后通分后利用整体思想计算.
| ||
| x |
| ||
| y |
解答:解:不正确.
∵x+y=-3<0,xy=2>0,
∴x<0,y<0,
∴原式=
+
=
+
=-
-
=-
•
=-
•
=
.
∵x+y=-3<0,xy=2>0,
∴x<0,y<0,
∴原式=
|
|
=
| ||
| |y| |
| ||
| |x| |
=-
| ||
| x |
| ||
| y |
=-
| xy |
| x+y |
| xy |
=-
| 2 |
| -3 |
| 2 |
=
3
| ||
| 2 |
点评:本题考查了二次根式的化简求值:先把二次根式进行化简或变形,然后运用整体思想进行计算.

练习册系列答案
相关题目
 .
.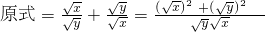 =
=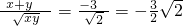 .
.