题目内容
如图，已知∠AOB=50°，OM平分∠AOB，MA⊥OA于A，MB⊥OB于B，则∠MAB=________．
25°
分析：根据已知推出∠MAO=∠MBO=90°，MA=MB，求出∠AMB=130°，推出∠MAB=∠MBA=
×（180°-∠AMB），代入求出即可．
解答：∵OM平分∠AOB，MA⊥OA，MB⊥OB，
∴∠MAO=∠MBO=90°，MA=MB，
∵∠AOB=50°，
∴∠AMB=360°-90°-90°-50°=130°，
∵MA=MB，
∴∠MAB=∠MBA=×（180°-∠AMB）=×（180°-135°）=25°，
故答案为：25°．
点评：本题考查了角平分线性质，三角形内角和定理，等腰三角形的性质和判定的应用，注意：角平分线上的点到角两边的距离相等．
分析：根据已知推出∠MAO=∠MBO=90°，MA=MB，求出∠AMB=130°，推出∠MAB=∠MBA=
×（180°-∠AMB），代入求出即可．解答：∵OM平分∠AOB，MA⊥OA，MB⊥OB，
∴∠MAO=∠MBO=90°，MA=MB，
∵∠AOB=50°，
∴∠AMB=360°-90°-90°-50°=130°，
∵MA=MB，
∴∠MAB=∠MBA=
×（180°-∠AMB）=×（180°-135°）=25°，故答案为：25°．
点评：本题考查了角平分线性质，三角形内角和定理，等腰三角形的性质和判定的应用，注意：角平分线上的点到角两边的距离相等．
练习册系列答案
相关题目
如图，已知∠AOB是直角，∠AOC是锐角，ON平分∠AOC，OM平分∠BOC，则∠MON是（ ）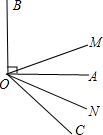
| A、45° | ||
B、45°+
| ||
C、60°-
| ||
| D、不能计算 |
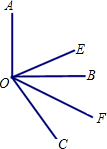如图，已知∠AOB是直角，∠BOC=60°，OE平分∠AOC，OF平分∠BOC．
尺规作图：
如图，已知∠AOB=x（0°＜x＜180°），OC平分∠AOB，点N为OB上一个定点．通过画图可以知道：当∠AOB=45°时，在射线OC上存在点P，使△ONP成为等腰三角形，且符合条件的点有三个，即P1（顶点为P2），P2（顶点为0），P3（顶点为N）．