题目内容
P是长方形ABCD的对角线BD上的一点，M为线段PC的中点．如果三角形APB的面积是2平方厘米，则三角形BCM的面积等于________平方厘米．
1
分析：首先连接AC交BD于O，则可得：S△ABO=S△CBO，S△APO=S△CPO．又由BM是△CBP的一条中线，即可求得三角形BCM的面积．
解答：
解：根据题意画图，如图所示．
连接AC交BD于O，
则S△ABO=S△CBO，S△APO=S△CPO．
∴S△ABP=S△CBP，
∵S△APB=2平方厘米，
∴S△CBP=2平方厘米．
∵BM是△CBP的一条中线，
∴S△BCM=1平方厘米．
点评：此题考查了有关三角形面积的知识与长方形的性质．注意三角形中线平分三角形的面积．
分析：首先连接AC交BD于O，则可得：S△ABO=S△CBO，S△APO=S△CPO．又由BM是△CBP的一条中线，即可求得三角形BCM的面积．
解答：
解：根据题意画图，如图所示．连接AC交BD于O，
则S△ABO=S△CBO，S△APO=S△CPO．
∴S△ABP=S△CBP，
∵S△APB=2平方厘米，
∴S△CBP=2平方厘米．
∵BM是△CBP的一条中线，
∴S△BCM=1平方厘米．
点评：此题考查了有关三角形面积的知识与长方形的性质．注意三角形中线平分三角形的面积．
练习册系列答案
名校课堂系列答案
相关题目
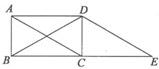8、如图，AC、BD是长方形ABCD的对角线，过点D作DE∥AC交BC的延长线于E，则图中与△ABC全等的三角形共有（ ）
11、如图所示，MN，PQ是长方形ABCD的两条对称轴，MN交AB于E，交CD于F，PQ交AD于H，交BC于G，若AB=3，BC=6，则四边形EGFH的面积为
19、如图，BD是长方形ABCD的一条对角线，CE⊥BD于点E．
如图，E是长方形ABCD的边BC上一点，沿AE折叠，顶点B刚好与CD上点F重合，若AD=16，BE=10，求AE．