题目内容
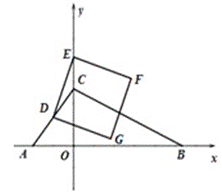
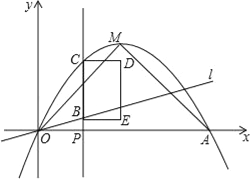
【题目】如图,抛物线y=﹣![]() x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=
x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=![]() x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.
x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.
【答案】![]() 或
或![]() 或
或![]() <a≤5.
<a≤5.
【解析】∵y=﹣![]() x2+2x=﹣
x2+2x=﹣![]() (x﹣4)2+4,∴顶点M的坐标为(4,4),
(x﹣4)2+4,∴顶点M的坐标为(4,4),
令y=0,则﹣![]() x2+2x=0,整理得,x2﹣8x=0,解得x1=0,x2=8,∴点A的坐标为(8,0),
x2+2x=0,整理得,x2﹣8x=0,解得x1=0,x2=8,∴点A的坐标为(8,0),
设直线AM的解析式为y=kx+b(k≠0),则![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+8,∴∠MAO=45°,由抛物线的对称性得,△AMO是等腰直角三角形,
①矩形BCDE为正方形时,BC=DC,∴(﹣![]() a2+2a)﹣
a2+2a)﹣![]() a=2,解得a1=
a=2,解得a1=![]() ,a2=
,a2=![]() ;
;
②矩形BCDE关于抛物线对称轴对称时,点P的横坐标a=4+![]() CD=4+
CD=4+![]() ×2=4+1=5;
×2=4+1=5;
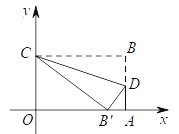
③如图,点E在AM上时,设直线y=![]() x与直线AM相交于点G,
x与直线AM相交于点G,
联立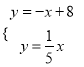 ,解得
,解得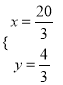 ,∴点G的坐标为(
,∴点G的坐标为(![]() ,
, ![]() ),
),
∵PB∥y轴,四边形BCDE为矩形,∴BE∥x轴,∴△GBE∽△OGA,
∴![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
过点G作GH⊥x轴于H,则GH∥PB,∴△OBP∽△OGH,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得PB=1,∴点B的纵坐标为1,
,解得PB=1,∴点B的纵坐标为1,
代入y=![]() x得,
x得, ![]() x=1,解得x=5,∴点P的横坐标a=5,
x=1,解得x=5,∴点P的横坐标a=5,
∴从此位置到点B与点G重合,重叠部分为等腰直角三角形,∴![]() <a≤5;
<a≤5;
综上所述,矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是: ![]() 或
或![]() 或5或
或5或![]() <a<5,故答案为
<a<5,故答案为![]() 或
或![]() 或
或![]() <a≤5.
<a≤5.

练习册系列答案
相关题目