题目内容

图①是一个边长为（m+n）的正方形，小颖将图①中的阴影部分拼成图②的形状，由图①和图②能验证的式子是


  1. A.
    （m+n）2-（m-n）2=4mn
  2. B.
    （m+n）2-（m2+n2）=2mn
  3. C.
    （m-n）2+2mn=m2+n2
  4. D.
    （m+n）（m-n）=m2-n2
B
分析：根据图示可知，阴影部分的面积是边长为m+n的正方形减去中间白色的正方形的面积m2+n2，即为对角线分别是2m，2n的菱形的面积．据此即可解答．
解答：（m+n）2-（m2+n2）=2mn．
故选B．
点评：本题是利用几何图形的面积来验证（m+n）2-（m2+n2）=2mn，解题关键是利用图形的面积之间的相等关系列等式．
练习册系列答案
相关题目
8、图1是一个边长为1的等边三角形和一个菱形的组合图形，菱形边长为等边三角形边长的一半，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），…，则第n个图形的周长是（　　）
（2012•广西模拟）图1是一个边长为1的等边三角形和一个菱形的组合图形，菱形边长为等边三角形边长的一半，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），…，则第2012个图形的周长是（　　）
作图题：
如图，是一个边长为1的正方形网格，请在网格中画出一个边长为2
2
，
5
和3的三角形．（要求三角形的顶点在小格的顶点处）．
同学们，学习了无理数之后，我们已经把数的领域扩大到了实数的范围，这说明我们的知识越来越丰富了！可是，无理数究竟是一个什么样的数呢？下面让我们在几个具体的图形中认识一下无理数．
（1）如图①△ABC是一个边长为2的等腰直角三角形．它的面积是2，把它沿着斜边的高线剪开拼成如图②的正方形ABCD，则这个正方形的面积也就等于正方形的面积即为2，则这个正方形的边长就是
2
，它是一个无理数．

（2）如图，直径为1个单位长度的圆从原点O沿数轴向右滚动一周，圆上的一点P（滚动时与点O重合）由原点到达点O′，则OO′的长度就等于圆的周长π，所以数轴上点O′代表的实数就是
π
π
，它是一个无理数．

（3）如图，在Rt△ABC中，∠C=90°，AC=2，BC=1，根据勾股定理可求得AB=
5
5
，它是一个无理数．

好了，相信大家对无理数是不是有了更具体的认识了，那么你是也试着在图形中作出两个无理数吧：
1、你能在6×8的网格图中（每个小正方形边长均为1），画出一条长为
10
的线段吗？

2、学习了实数后，我们知道数轴上的点与实数是一一对应的关系．那么你能在数轴上找到表示 -
5
的点吗？
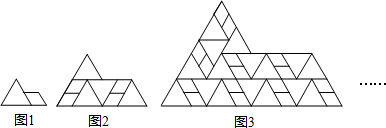图1是一个边长为2的等边三角形和一个四边均长为1的四边形的组合图形，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），…，则第1个图形的周长是
8
8
；第4个图形的周长是
64
64
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网