题目内容
6. 如图所示,△ABC是直角三角形,△FAC是直角三角形,已知AB=4cm,AF=12cm,BC=3cm,求以FC为边长的正方形的面积.
如图所示,△ABC是直角三角形,△FAC是直角三角形,已知AB=4cm,AF=12cm,BC=3cm,求以FC为边长的正方形的面积.
分析 先由勾股定理求出AC,再由勾股定理求出CF,即可得出所求正方形的面积.
解答 解:∵,△ABC是直角三角形,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5(cm),
∵△FAC是直角三角形,
∴CF=$\sqrt{A{C}^{2}+A{E}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13(cm),
∴以FC为边长的正方形的面积=CF2=169(cm2).
点评 本题考查了勾股定理、正方形面积的计算;熟练掌握勾股定理,由勾股定理求出CF是解决问题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
16.在-4,0,2.5,|-3|这四个数中,最大的数是( )
| A. | -4 | B. | 0 | C. | 2.5 | D. | |-3| |
14. 某校七年级学生总人数为800,其男女生所占比例如图所示,则该校七年级男生人数为( )
某校七年级学生总人数为800,其男女生所占比例如图所示,则该校七年级男生人数为( )
 某校七年级学生总人数为800,其男女生所占比例如图所示,则该校七年级男生人数为( )
某校七年级学生总人数为800,其男女生所占比例如图所示,则该校七年级男生人数为( )| A. | 500 | B. | 400 | C. | 384 | D. | 416 |
15.若m2-2m=1,则2m2-4m+2013=( )
| A. | 2013 | B. | 2014 | C. | 2015 | D. | 2016 |
 如图,在Rt△ABC中,∠C=90°,BC=6,sinA=0.6,求cosA、tanB的值.
如图,在Rt△ABC中,∠C=90°,BC=6,sinA=0.6,求cosA、tanB的值.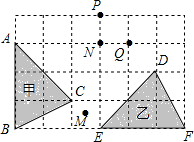 如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是(P,N,Q都是格点,M是小正方形的中心)( )
如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是(P,N,Q都是格点,M是小正方形的中心)( )