��Ŀ����
��ͼ��ʾ��������ABCD�У���֪AB��DC�� AD��DB��AD=DC=CB��
AB=4����AB����ֱ��Ϊ �ᣬ��D�Ҵ�ֱ��AB��ֱ��Ϊ
�ᣬ��D�Ҵ�ֱ��AB��ֱ��Ϊ �Ὠ��ƽ��ֱ������ϵ��
�Ὠ��ƽ��ֱ������ϵ��
��С��1����1�����DAB�Ķ�����A��D��C��������ꣻ
��С��2����2�����A��D��C����������ߵĽ���ʽ����
�Գ���L��
��С��3����3����P�������ߵĶԳ���L�ϵĵ㣬��ôʹ PDBΪ���������εĵ�P�м���?
PDBΪ���������εĵ�P�м���?
���������P�����ֻ꣬��˵���������ɣ�
����1����1�� ��DC��AB��AD=DC=CB��
�� ��CDB=��CBD=��DBA��
��DAB=��CBA��
���DAB=2��DBA��
�ߡ�DAB+��DBA=90 ��
��
���D AB=60
AB=60 ��������3��
��������3��
�ߡ�DBA=30 �� AB=4��
�� AB=4��
��DC=AD=2��
Rt��AOD��OA=1��OD= ��
��
��A��-1��0����D��0�� ����C��2��
����C��2�� ����
����
��С��2����2������֪�ã����������������߱ع���A��-1��0����B��3��0����D��0��  ��
��
�ʿ�������Ϊ  =
= x2+bx+c ����������6��
x2+bx+c ����������6��
��������������ʽ��  , ��ã�
, ��ã�
���������ߵĽ���ʽΪ  =
= 
 ����������9��
����������9��
��Գ���LΪֱ�� =1��
=1��
��С��3����3��ʹ PDBΪ������
PDBΪ������ ���εĵ�P��5������������12��
���εĵ�P��5������������12�� PDBΪ���������Σ����������������
PDB�������������������������
����ֱ��L��DB��ƽ�У�DB�Ĵ�ֱƽ������L����һ������P1��P1D=P1B��  P1DBΪ���������Σ�
P1DB����������
����Ϊ��DΪԲ�ģ�DBΪ�뾶��Բ��ֱ��L����������P2��P3��DB=DP2��DB=DP3��  P2DB��
P2DB��  P3DB����������
P3DB����������
�����ͬ����L��Ҳ��������P4��P5��ʹ�� BD=BP4��BD=BP5��
�������ϸ��㻥���غϣ�������ֱ��L�ϣ�ʹ PDBΪ���������εĵ�P��5��
PDBΪ���������εĵ�P��5��
����

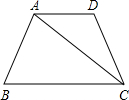 ��֪��ͼ��ʾ��������ABCD�У�AD��BC��AB=AD=DC=8����B=60�㣬����AC��
��֪��ͼ��ʾ��������ABCD�У�AD��BC��AB=AD=DC=8����B=60�㣬����AC��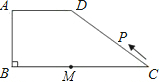 ��ͼ��ʾ��������ABCD�У�AD��BC����ABC=90�㣬AD=AB=6��BC=14����M���߶�BC��һ���㣬��MC=8������P��C�������C?D?A?B��·���˶����˶�����Bֹͣ���ڵ�P���˶������У�ʹ��PMCΪ���������εĵ�P��
��ͼ��ʾ��������ABCD�У�AD��BC����ABC=90�㣬AD=AB=6��BC=14����M���߶�BC��һ���㣬��MC=8������P��C�������C?D?A?B��·���˶����˶�����Bֹͣ���ڵ�P���˶������У�ʹ��PMCΪ���������εĵ�P��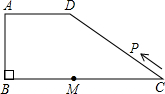 ��ͼ��ʾ��������ABCD�У�AD��BC����ABC=90�㣬AD=AB=6��BC=14����M���߶�BC��һ���㣬��MC=8������P��C�������C��D��A��B��·���˶����˶�����Bֹͣ���ڵ�P���˶������У�ʹ��PMCΪ���������εĵ�P�м������������Ӧ���������ε�������
��ͼ��ʾ��������ABCD�У�AD��BC����ABC=90�㣬AD=AB=6��BC=14����M���߶�BC��һ���㣬��MC=8������P��C�������C��D��A��B��·���˶����˶�����Bֹͣ���ڵ�P���˶������У�ʹ��PMCΪ���������εĵ�P�м������������Ӧ���������ε�������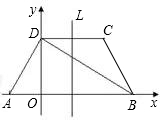 ��ͼ��ʾ��������ABCD�У���֪AB��CD��AD��DB��AD=DC=CB��AB=4��DO��ֱ��AB����������
��ͼ��ʾ��������ABCD�У���֪AB��CD��AD��DB��AD=DC=CB��AB=4��DO��ֱ��AB���������� ��ͼ��ʾ��������ABCD�У�AB��DC��EF�����ε���λ�ߣ�AC��EF��G��BD��EF��H������˵��������ǣ�������
��ͼ��ʾ��������ABCD�У�AB��DC��EF�����ε���λ�ߣ�AC��EF��G��BD��EF��H������˵��������ǣ�������