题目内容
已知二次函数y=-x2+2x+3的图象向左平移1个单位，再向下平移2个单位，求平移后的抛物线的解析式．
考点：二次函数图象与几何变换
专题：
分析：先将抛物线y=-x2+2x+3化为顶点坐标式，再按照“左加右减，上加下减”的规律平移则可．
解答：解：根据题意，y=-x2+2x+3=-（x-1）2+4，向左平移1个单位，再向下平移2个单位，得y=-（x-1+1）2+4-2，即y=-x2+2．
即平移后的抛物线的解析式为y=-x2+2．
即平移后的抛物线的解析式为y=-x2+2．
点评：此题考查了二次函数图象与几何变换以及一般式转化顶点式，正确将一般式转化为顶点式是解题关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
数轴上点A表示的数是-1，将点A沿数轴移动2个单位到点B，则点B所表示的数是（ ）
| A、-3 | B、1 |
| C、-1或3 | D、-3或1 |
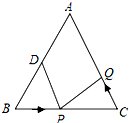如图，已知△ABC中，AB=AC=20cm，∠ABC=∠ACB，BC=16cm，点D是AB的中点．点P在线段BC上以6厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动，且点Q的运动速度与点P的运动速度相等．经过1秒后，△BPD与△CQP是否全等，请说明理由．下列说法中不正确的是（ ）
A、
| ||
B、
| ||
| C、27的立方根是3 | ||
| D、立方根等于-1的实数是-1 |
若ab≠0，则
+
的值不可能是（ ）
| a |
| |a| |
| |b| |
| b |
| A、2 | B、0 | C、-2 | D、1 |
？