Question

如图，⊙O的半径为2，∠BAC=30°，则图中的BC长为________．

Answer 1

2
分析：首先连接OB，OC，由∠BAC=30°，根据在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠BOC=60°，易得△OBC是等边三角形，继而求得BC的长．
解答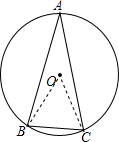：解：连接OB，OC．
∵∠BAC=30°，
∴∠BOC=2∠BAC=60°，
∵OB=OC，
∴△OBC是等边三角形，
∴BC=OB=OC=2．
故答案为：2．
点评：此题考查了圆周角定理与等边三角形的判定与性质．此题比较简单，注意掌握辅助线的作法，注意在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用．