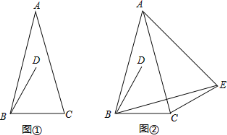
题目内容
对于平面直角坐标系中的任意两点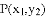 ,
,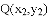 ,我们把
,我们把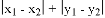 叫
叫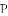
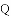
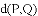
(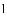
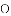
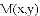
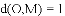
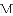
(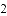
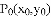 是平面上一点,
是平面上一点,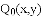 是直线
是直线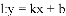
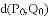 的最小值叫做
的最小值叫做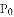 到直线
到直线
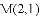
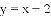
(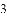




试求直线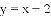

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目


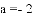
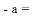
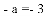
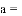
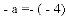
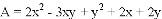 ,
,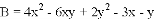
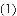
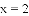
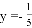 时,求
时,求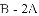
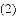
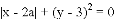 ,且
,且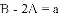
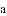
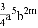 与
与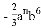 的和是一个单项式,则
的和是一个单项式,则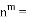 ________.
________. 的正确结果是( )
的正确结果是( ) C.
C.  D.
D. 
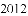
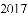
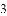
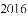
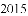
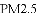
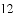
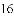
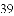
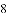
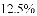
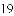
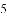
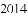
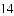
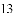
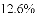
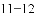
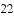
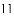
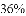
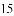
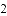
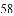
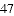
 )
)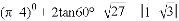 .
.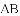
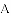
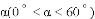 得到线段
得到线段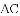
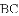
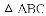
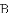
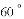 得线段
得线段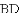
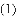
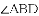
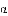
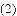
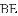
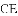
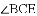
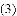
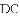
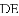
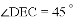 .
.