题目内容
2.如图①是汽车后窗雨刮器示意图,橡皮条AB绕点O逆时针旋转90°,O、A、B在一条直线上,如图②将OAB折弯,使∠OAB=120°,橡皮条AB绕点O逆时针旋转90°,其中AB=20cm,OA=10cm(1)求图①中橡皮条AB刮过的面积;
(2)在图②中
①求点O到AB的距离;
②求橡皮条AB刮过的面积;
(3)如图③,将图的阴影部分放入一个矩形AEFG内,其中B在AF上,D在FG上,$\widehat{BD}$与EF相切,直接写出矩形AEFG的长和宽.

分析 (1)如图①,根据S阴影部分=S扇形OBD-S扇形OAC计算即可;
(2)①如图2中,作OH⊥BA于H.根据OH=OA•sin60°计算即可;
②根据题意,得∠1=∠2,由圆心角都为90°的扇形OAC与扇形OBD得到,OA=OC,OB=OD,于是△OAB≌△OCD,S扇形OCE=S扇形OAF,
得到S曲边DEC=S曲边ABF,则S阴影部分=S曲边DEFB=S扇形OBD-S扇形OEF,由此计算即可;
(3)如图3中,作OM⊥BF于M交AG于N,作CH⊥OM于H.在Rt△COH中,OC=10,∠OCH=60°,求出CH=$\frac{1}{2}$OC=5,在Rt△AON中,由AO=10,∠OAN=30°,求出ON,AN即可解决问题;
解答 解:(1)如图①
S阴影部分=S扇形OBD-S扇形OAC=$\frac{90π•3{0}^{2}}{360}$-$\frac{90π•1{0}^{2}}{360}$=200π
(2)①如图2中,作OH⊥BA于H.
在Rt△OAH中,∵∠OAH=60°,OA=10,∠H=90°,
∴OH=OA•sin60°=5$\sqrt{3}$.
∴点O到AB的距离为5$\sqrt{3}$.
②根据题意,得∠1=∠2,
由圆心角都为90°的扇形OAC与扇形OBD得到,OA=OC,OB=OD,
于是△OAB≌△OCD,S扇形OCE=S扇形OAF,
得到S曲边DEC=S曲边ABF,
则S阴影部分=S曲边DEFB=S扇形OBD-S扇形OEF=200π.
(3)如图3中,作OM⊥BF于M交AG于N,作CH⊥OM于H.
易知OM=20+10=30,
在Rt△COH中,OC=10,∠OCH=60°,
∴CH=$\frac{1}{2}$OC=5,
在Rt△AON中,∵AO=10,∠OAN=30°,
∴ON=$\frac{1}{2}$OA=5,AN=5$\sqrt{3}$,
∴FG=MN=OM-ON=30-5=25,AG=CD+CH+AN=20+5+5$\sqrt{3}$=25+5$\sqrt{3}$,
∴矩形AEFG的长和宽分别为25+5$\sqrt{3}$和25.
点评 本题考查圆综合题、扇形的面积、全等三角形的判定和性质等知识,解题的关键是学会把不规则图形转化为规则图形解决,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.

| 职工 | 甲 | 乙 |
| 月销售件数(件) | 200 | 180 |
| 月工资(元) | 1800 | 1700 |
(2)若职工丙今年5月份的工资为2000元,那么丙该月销售了多少件产品?
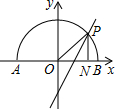 如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )
如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )| A. | (0,-1) | B. | (0,-$\frac{4}{5}$) | C. | (0,-$\frac{3}{5}$) | D. | (0,-$\frac{6}{5}$) |
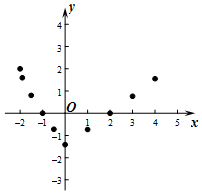 有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?
有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?小军根据学习函数的经验,对函数y=-$\sqrt{x+2}$+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=-$\sqrt{x+2}$+|x|的自变量x的取值范围是x≥-2;
(2)表是y与x的几组对应值?
| x | -2 | -1.9 | -1.5 | -1 | -0.5 | 0 | 1 | 2 | 3 | 4 | … |
| y | 2 | 1.60 | 0.80 | 0 | -0.72 | -1.41 | -0.37 | 0 | 0.76 | 1.55 | … |
(3)观察图象,函数的最小值是-$\sqrt{2}$;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外):当-2≤x<0时,y随x的增大而减小.

 某中学为了解学生到校交通方式情况,随机抽取各年级部分学生就“上下学交通方式”进行问卷调查,调查分为“A:骑自行车;B:不行;C:坐公交车;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2),请根据图中的信息,解答下列问题:
某中学为了解学生到校交通方式情况,随机抽取各年级部分学生就“上下学交通方式”进行问卷调查,调查分为“A:骑自行车;B:不行;C:坐公交车;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2),请根据图中的信息,解答下列问题:
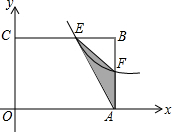 如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)的图象与BC边交于点E.
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)的图象与BC边交于点E.